–≠–Ľ–Ľ–ł–Ņ—Ā, –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į, –Ņ–į—Ä–į–Ī–ĺ–Ľ–į.¬†–Ē–ł—Ä–Ķ–ļ—ā–ĺ—Ä–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ —ć–Ľ–Ľ–ł–Ņ—Ā–į –ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č.¬†
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į: –°–Ī–ĺ—Ä–Ĺ–ł–ļ –∑–į–ī–į—á –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ. –ß–į—Ā—ā—Ć 1. –ü–ĺ–ī —Ä–Ķ–ī –ź. –í. –ē—Ą–ł–ľ–ĺ–≤–į, –Ď. –ü. –Ē–Ķ–ľ–ł–ī–ĺ–≤–ł—á–į.
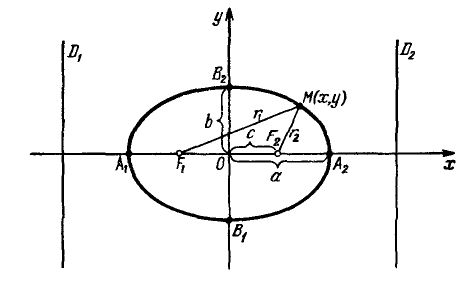
–≠–Ľ–Ľ–ł–Ņ—Ā.
–≠–Ľ–Ľ–ł–Ņ—Ā —Ā –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1, a\geq b>0,$ –ł–ľ–Ķ–Ķ—ā —Ą–ĺ—Ä–ľ—ɬ†–ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–Ĺ—É—é –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–ü–į—Ä–į–ľ–Ķ—ā—Ä—č $a$ –ł $b$ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –Ņ–ĺ–Ľ—É–ĺ—Ā—Ź–ľ–ł —ć–Ľ–Ľ–ł–Ņ—Ā–į (–Ī–ĺ–Ľ—Ć—ą–ĺ–Ļ –ł –ľ–į–Ľ–ĺ–Ļ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ). –Ę–ĺ—á–ļ–ł $A_1(-a, 0),$¬†$A_2(a, 0), $¬†$B_1(0, -b), $¬†–ł $B_2(0, b), $ –Ķ–≥–ĺ –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł. –ě—Ā–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł $Ox$ –ł $Oy$ - –≥–Ľ–į–≤–Ĺ—č–ľ–ł –ĺ—Ā—Ź–ľ–ł –į —Ü–Ķ–Ĺ—ā—Ä —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł $O -$¬†—Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ —ć–Ľ–Ľ–ł–Ņ—Ā–į.
–Ę–ĺ—á–ļ–ł $F_1(-c, 0)$ –ł $F_2(c, 0),$ –≥–ī–Ķ $c=\sqrt{a^2-b^2}\geq 0,$ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ą–ĺ–ļ—É—Ā–į–ľ–ł —ć–Ľ–Ľ–ł–Ņ—Ā–į –≤–Ķ–ļ—ā–ĺ—Ä—č $\overline{F_1M}$ –ł $\overline{F_2M} -$ —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ–ł —Ä–į–ī–ł—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł, ¬†–į —á–ł—Ā–Ľ–į $r_1=|\overline{F_1M}|$ –ł¬†$r_2=|\overline{F_2M}| -$¬†—Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ–ł —Ä–į–ī–ł—É—Ā–į–ľ–ł —ā–ĺ—á–ļ–ł $M,$ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—Č–Ķ–Ļ —ć–Ľ–Ľ–ł–Ņ—Ā—É. –í —á–į—Ā—ā–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ $a=b$ —Ą–ĺ–ļ—É—Ā—č $F_1$ –ł $F_2$ —Ā–ĺ–≤–Ņ–į–ī–į—é—ā —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ, –į –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ł–ľ–Ķ–Ķ—ā –≤–ł–ī¬†$\frac{x^2}{a^2}+\frac{y^2}{a^2}=1,$¬†–ł–Ľ–ł $x^2+y^2=a^2,$ —ā.–Ķ. –ĺ–Ņ–ł—Ā—č–≤–į–Ķ—ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ä–į–ī–ł—É—Ā–į $a$ —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā.¬†
–ß–ł—Ā–Ľ–ĺ $e=\frac{c}{a}=\sqrt{1-\frac{b^2}{a^2}} \,\, (0\leq e<1)$ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā–ĺ–ľ —ć–Ľ–Ľ–ł–Ņ—Ā–į –ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ľ–Ķ—Ä–ĺ–Ļ –Ķ–≥–ĺ "—Ā–Ņ–Ľ—é—Ā–Ĺ—É—ā–ĺ—Ā—ā–ł" (–Ņ—Ä–ł $e=0$ —ć–Ľ–Ľ–ł–Ņ—Ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć—é.)
–ü—Ä—Ź–ľ—č–Ķ $D_1: x=-a/e$ –ł $D_2: x=a/e,$ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –≥–Ľ–į–≤–Ĺ–ĺ–Ļ –ĺ—Ā–ł –ł –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł $a/e$ –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į, –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā–į–ľ–ł —ć–Ľ–Ľ–ł–Ņ—Ā–į.
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į.¬†(–Ē–ł—Ä–Ķ–ļ—ā–ĺ—Ä–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ —ć–Ľ–Ľ–ł–Ņ—Ā–į)
–≠–Ľ–Ľ–ł–Ņ—Ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ–ľ —ā–ĺ—á–Ķ–ļ, –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ –ĺ—ā –ļ–ĺ—ā–ĺ—Ä—č—Ö –ī–ĺ —Ą–ĺ–ļ—É—Ā–į –ł –ī–ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā—č –Ņ–ĺ—Ā—ā–ĺ—Ź–ŖŖ嬆–ł —Ä–į–≤–Ĺ–ĺ $e.$
–ü—Ä–ł–ľ–Ķ—Ä—č.
2.246. –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć —ć–Ľ–Ľ–ł–Ņ—Ā $9x^2+25y^2=225.$ –Ě–į–Ļ—ā–ł: –į) –Ņ–ĺ–Ľ—É–ĺ—Ā–ł; –Ī) –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ą–ĺ–ļ—É—Ā–ĺ–≤; –≤) —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā; ¬†–≥) —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü—Ä–ł–≤–Ķ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ľ–ł–Ņ—Ā–į –ļ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–ľ—É –≤–ł–ī—É:
$$ 9x^2+25y^2=225 |:225\Rightarrow\frac{9x^2}{225}+\frac{25y^2}{225}=1\Rightarrow$$
$$\Rightarrow\frac{x^2}{25}+\frac{y^2}{9}=1\Rightarrow\frac{x^2}{5^2}+\frac{y^2}{3^2}=1.$$
–į) –Ě–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł $a=5,$ $b=3.$
–Ī) –§–ĺ–ļ—É—Ā—č –Ĺ–į–Ļ–ī–Ķ–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$F_1(-c, 0)$ –ł $F_2(c, 0),$ –≥–ī–Ķ $c=\sqrt{a^2-b^2}:$
$c=\sqrt{5^2-3^2}=\sqrt{16}=4\Rightarrow F_1(-4, 0),\qquad F_2(4, 0).$
–≤) –≠–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā $e=\frac{c}{a}=\frac{4}{5}.$
–≥) –£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
¬†$D_1: x=-\frac{5}{4/5}=-\frac{25}{4}$ –ł $D_2: x=\frac{5}{4/5}=\frac{25}{4}.$
–°–ī–Ķ–Ľ–į–Ķ–ľ —Ä–ł—Ā—É–Ĺ–ĺ–ļ:
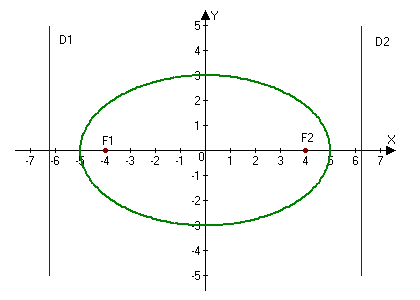
–ě—ā–≤–Ķ—ā:¬†–į) ¬†$a=5,$ $b=3;$¬†–Ī)¬†$ F_1(-4, 0),\qquad F_2(4, 0);$¬†–≤) $e=\frac{4}{5};$¬†–≥)¬†$D_1: x=-\frac{25}{4}$ –ł $D_2: x=\frac{25}{4}.$
  {jumi[*3]}
2.249 (a). –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć, —á—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ $5x^2+9y^2-30x+18y+9=0$ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā —ć–Ľ–Ľ–ł–Ņ—Ā, –Ĺ–į–Ļ—ā–ł –Ķ–≥–ĺ —Ü–Ķ–Ĺ—ā—Ä $C,$ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł, —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā –ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
¬†–ü—Ä–ł–≤–Ķ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ľ–ł–Ņ—Ā–į –ļ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–ľ—É –≤–ł–ī—É, –ī–Ľ—Ź —ć—ā–ĺ–≥–ĺ –≤—č–ī–Ķ–Ľ–ł–ľ –Ņ–ĺ–Ľ–Ĺ—č–Ķ –ļ–≤–į–ī—Ä–į—ā—č:¬†
$$5x^2+9y^2-30x+18y+9=(5x^2-30x)+(9y^2+18y)+9=$$
$$5(x^2+6x+9-9)+9(y^2+2y+1-1)+9=5(x+3)^2-45+9(y+1)^2-9+9=$$
$$5(x+3)^2+9(y+1)^2-45=0\Rightarrow5(x+3)^2+9(y+1)^2=45|:45\Rightarrow$$
$$ \frac{(x+3)^2}{9}+\frac{(y+1)^2}{5}=1\Rightarrow\frac{(x+3)^2}{3^2}+\frac{(y+1)^2}{(\sqrt 5)^2}=1.$$
–≠—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ľ–ł–Ņ—Ā–į. –¶–Ķ–Ĺ—ā—Ä –ł–ľ–Ķ–Ķ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $C=(x_0, y_0)=(-3, -1);$ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł $a=3,$ $b=\sqrt 5.$
$c=\sqrt{a^2-b^2}\Rightarrow c=\sqrt{9-5}=\sqrt 4=2\Rightarrow e=\frac{c}{a}=\frac{2}{3}.$
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā –ī–Ľ—Ź —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
¬†$D_1: x=-\frac{3}{2/3}=-\frac{9}{2} $ –ł $D_2: x=\frac{3}{2/3}=\frac{9}{2}.$ –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —É –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ü–Ķ–Ĺ—ā—Ä —Ā–ľ–Ķ—Č–Ķ–Ĺ, —ā–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā—Ā—č –Ī—É–ī—É—ā –ł–ľ–Ķ—ā—Ć —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź¬†$D_1: x=x_0-a/e$ –ł $D_2: x=x_0+a/e:$
$$D_1: x=3-\frac{9}{2}=\frac{6-9}{2}=-\frac{3}{2}\Rightarrow 2x+3=0 $$  $$D_2: x=3+\frac{9}{2}=\frac{6+9}{2}=\frac{15}{2}\Rightarrow2x-15=0.$$
–ě—ā–≤–Ķ—ā:¬†$C=(x_0, y_0)=(-3, -1);$ ¬†$a=3,$ $b=\sqrt 5;$¬†$ e=\frac{2}{3}.$¬†$D_1:2x+3=0, $ $D_2: 2x-15=0.$
 
2.252. –≠–Ľ–Ľ–ł–Ņ—Ā, –≥–Ľ–į–≤–Ĺ—č–Ķ –ĺ—Ā–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —Ā–ĺ–≤–Ņ–į–ī–į—é—ā —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ—č–ľ–ł –ĺ—Ā–ľ–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł $M_1(2, \sqrt 3)$ –ł $M_2(0, 2).$ –Ě–į–Ņ–ł—Ā–į—ā—Ć –Ķ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ, –Ĺ–į–Ļ—ā–ł —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ķ —Ä–į–ī–ł—É—Ā—č —ā–ĺ—á–ļ–ł $M_1$ –ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł –ī–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –ĺ—Ā–ł —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ā–ĺ–≤–Ņ–į–ī–į—é—ā —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ—č–ľ–ł –ĺ—Ā—Ź–ľ–ł, —ā–ĺ —Ü–Ķ–Ĺ—ā—Ä —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā –Ĺ–į—á–į–Ľ–ĺ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ł–∑ —ā–ĺ–≥–ĺ, —á—ā–ĺ —ā–ĺ—á–ļ–į $(0, 2)$ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł—ā —ć–Ľ–Ľ–ł–Ņ—Ā—É, –ľ–ĺ–∂–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć –≤—č–≤–ĺ–ī, —á—ā–ĺ $b=2.$
–Ē–į–Ľ–Ķ–Ķ, —á—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł $a,$ –Ņ–ĺ–ī—Ā—ā–į–≤–ł–ľ –Ĺ–į–Ļ–ī–Ķ–Ĺ–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ $b$ –ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł $M_1(2, \sqrt 3)$ –≤ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ľ–ł–Ņ—Ā–į¬†$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1:$
$$\frac{2^2}{a^2}+\frac{(\sqrt 3)^2}{2^2}=1\Rightarrow \frac{4}{a^2}+\frac{3}{4}=1\Rightarrow \frac{4}{a^2}=\frac{1}{4}\Rightarrow a^2=16\Rightarrow a=4.$$
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ľ–Ľ–ł–Ņ—Ā–į¬†$\frac{x^2}{16}+\frac{y^2}{4}=1.$
–Ē–į–Ľ–Ķ–Ķ –Ĺ–į–Ļ–ī–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ą–ĺ–ļ—É—Ā–ĺ–≤:
$c=\sqrt{a^2-b^2}=\sqrt{16-4}=2\sqrt 3\Rightarrow F_1(-2\sqrt 3, 0),\,\,\, F_2(2\sqrt 3, 0).$
–ě—ā—Ā—é–ī–į –Ĺ–į—Ö–ĺ–ī–ł–ľ $\overline {F_1M_1}=(2+2\sqrt 3, \sqrt 3),$¬†$\overline{F_2M_1}=(2-2\sqrt 3, \sqrt 3).$¬†
–°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ,¬†$r_1=|\overline {F_1M_1}|=\sqrt{(2+2\sqrt 3)^2+ (\sqrt 3)^2}=\sqrt{4+8\sqrt 3+12+3}=$ $=\sqrt{16+8\sqrt 3+3}=\sqrt{(4+\sqrt 3)^2}=4+\sqrt 3,$
$r_2=|\overline {F_2M_1}|=\sqrt{(2-2\sqrt 3)^2+ (\sqrt 3)^2}=\sqrt{4-8\sqrt 3+12+3}=$ $=\sqrt{16-8\sqrt 3+3}=\sqrt{(4-\sqrt 3)^2}=4-\sqrt 3.$
–ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł $M_1$ –ī–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā, –Ĺ–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā¬†–Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
$e=\frac{c}{a}=\frac{2\sqrt 3}{4}=\frac{\sqrt 3}{2};$
$D_1: x=-\frac{4}{\frac{\sqrt 3}{2}}=-\frac{8}{\sqrt 3}\Rightarrow \sqrt 3 x+8=0;$
$D_2: x=\frac{4}{\frac{\sqrt 3}{2}}=\frac{8}{\sqrt 3}\Rightarrow \sqrt 3 x-8=0.$
–†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $P(x_0, y_0)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ $L: Ax+By+C=0$¬†–≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $M_1(2, \sqrt 3)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ¬†$D_1: \sqrt 3 x+8=0$
$$d_1=\left|\frac{2\sqrt 3+8}{\sqrt{(\sqrt 3)^2}}\right|=\frac{2\sqrt 3+8}{\sqrt 3};$$
—Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $M_1(2, \sqrt 3)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ¬†$D_2: \sqrt 3 x-8=0$
$$d_2=\left|\frac{2\sqrt 3-8}{\sqrt{(\sqrt 3)^2}}\right|=\frac{8-2\sqrt 3}{\sqrt 3}.$$
–ě—ā–≤–Ķ—ā:¬†$\frac{x^2}{16}+\frac{y^2}{4}=1,$¬†$r_1=4+\sqrt 3,$¬†$r_2=4-\sqrt 3,$¬†$d_1=\frac{8+2\sqrt 3}{\sqrt 3},$¬†$d_2=\frac{8-2\sqrt 3}{\sqrt 3}.$
 
–ď–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į.
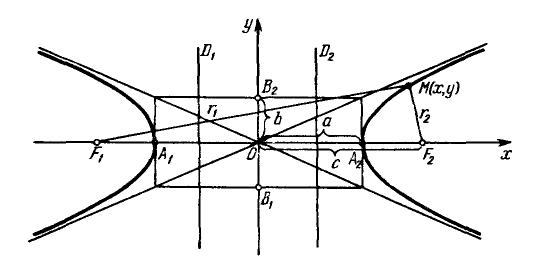
–ü–į—Ä–į–ľ–Ķ—ā—Ä—č $a$ –ł $b$ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –Ņ–ĺ–Ľ—É–ĺ—Ā—Ź–ľ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č. –Ę–ĺ—á–ļ–ł $A_1(-a, 0),$¬†$A_2(a, 0) - $¬†–Ķ–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–į–ľ–ł. –ě—Ā–ł —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł $Ox$ –ł $Oy$ - –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ł –ľ–Ĺ–ł–ľ–ĺ–Ļ –ĺ—Ā—Ź–ľ–ł –į —Ü–Ķ–Ĺ—ā—Ä —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–ł $O -$¬†—Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č.
–ü—Ä—Ź–ľ—č–Ķ $y=\pm\frac{b}{a}x$ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–į–ľ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č.
–Ę–ĺ—á–ļ–ł $F_1(-c, 0)$ –ł $F_2(c, 0),$ –≥–ī–Ķ $c=\sqrt{a^2+b^2}\geq 0,$ –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź —Ą–ĺ–ļ—É—Ā–į–ľ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č, –≤–Ķ–ļ—ā–ĺ—Ä—č $\overline{F_1M}$ –ł $\overline{F_2M} -$ —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ–ł —Ä–į–ī–ł—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–į–ľ–ł, ¬†–į —á–ł—Ā–Ľ–į $r_1=|\overline{F_1M}|$ –ł¬†$r_2=|\overline{F_2M}| -$¬†—Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ–ł —Ä–į–ī–ł—É—Ā–į–ľ–ł —ā–ĺ—á–ļ–ł $M,$ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—Č–Ķ–Ļ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–Ķ.¬†
–ß–ł—Ā–Ľ–ĺ $e=\frac{c}{a}=\sqrt{1+\frac{b^2}{a^2}} \,\, (1<e<+\infty)$ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā–ĺ–ľ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č –ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ľ–Ķ—Ä–ĺ–Ļ –Ķ–Ķ "—Ā–Ņ–Ľ—é—Ā–Ĺ—É—ā–ĺ—Ā—ā–ł". –í —á–į—Ā—ā–Ĺ–ĺ–ľ —Ā–Ľ—É—á–į–Ķ $a=b$ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ļ; –Ķ–Ķ —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā —Ä–į–≤–Ķ–Ĺ $e=\sqrt{2},$ –į —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–į–ľ–ł —Ä–į–≤–Ķ–Ĺ $\pi/2.$
–ü—Ä—Ź–ľ—č–Ķ $D_1: x=-a/e$ –ł $D_2:x=a/e,$ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č–Ķ –≥–Ľ–į–≤–Ĺ–ĺ–Ļ –ĺ—Ā–ł –ł –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł $a/e$ –ĺ—ā —Ü–Ķ–Ĺ—ā—Ä–į, –Ĺ–į–∑—č–≤–į—é—ā—Ā—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā–į–ľ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č.¬†
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į.¬†(–Ē–ł—Ä–Ķ–ļ—ā–ĺ—Ä–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č).
–ď–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–ľ –ľ–Ķ—Ā—ā–ĺ–ľ¬†—ā–ĺ—á–Ķ–ļ, –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ –ĺ—ā –ļ–ĺ—ā–ĺ—Ä—č—Ö –ī–ĺ —Ą–ĺ–ļ—É—Ā–į –ł –ī–ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā—č –Ņ–ĺ—Ā—ā–ĺ—Ź–ŖŖ嬆–ł —Ä–į–≤–Ĺ–ĺ $e.$
 
–ü—Ä–ł–ľ–Ķ—Ä—č.
2.265.¬†–ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—É $16x^2-9y^2=144.$ –Ě–į–Ļ—ā–ł: –į) –Ņ–ĺ–Ľ—É–ĺ—Ā–ł; –Ī) –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ą–ĺ–ļ—É—Ā–ĺ–≤; –≤) —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā; ¬†–≥) —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –į—Ā–ł–ľ–Ņ—ā–ĺ—ā; –ī) —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü—Ä–ł–≤–Ķ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č –ļ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–ľ—É –≤–ł–ī—É:
$$ 16x^2-9y^2=144 |:144\Rightarrow\frac{16x^2}{144}-\frac{9y^2}{144}=1\Rightarrow$$
$$\Rightarrow\frac{x^2}{9}-\frac{y^2}{16}=1\Rightarrow\frac{x^2}{3^2}+\frac{y^2}{4^2}=1.$$
–į) –Ě–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł $a=3,$ $b=4.$
–Ī) –§–ĺ–ļ—É—Ā—č –Ĺ–į–Ļ–ī–Ķ–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$F_1(-c, 0)$ –ł $F_2(c, 0),$ –≥–ī–Ķ $c=\sqrt{a^2+b^2}:$
$c=\sqrt{3^2+4^2}=\sqrt{25}=5\Rightarrow F_1(-5, 0),\qquad F_2(5, 0).$
–≤) –≠–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā $e=\frac{c}{a}=\frac{5}{3}.$
–≥) –ź—Ā–ł–ľ–Ņ—ā–ĺ—ā—č –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$y=\pm\frac{b}{a}x:$¬†
$$y=\pm\frac{4}{3}x.$$
–ī) –£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
¬†$D_1: x=-\frac{3}{5/3}=-\frac{9}{5}$ –ł $D_2: x=\frac{3}{5/3}=\frac{9}{5}.$
–°–ī–Ķ–Ľ–į–Ķ–ľ —Ä–ł—Ā—É–Ĺ–ĺ–ļ:
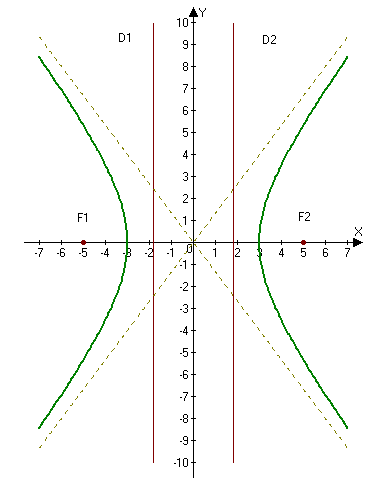
–ě—ā–≤–Ķ—ā:¬†–į)¬†¬†$a=3,$ $b=4;$¬†–Ī)¬†$ F_1(-5, 0),\qquad F_2(5, 0);$¬†–≤)¬†$e=\frac{5}{3};$ –≥)¬†$y=\pm\frac{4}{3}x;$¬†–ī)¬†$D_1: x=-\frac{9}{5}$ –ł $D_2: x=\frac{9}{5}.$
 
2.269 (a).¬†–£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć, —á—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ $16x^2-9y^2-64x-54y-161=0$ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—É, –Ĺ–į–Ļ—ā–ł –Ķ–Ķ —Ü–Ķ–Ĺ—ā—Ä $C,$ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł, —ć–ļ—Ā—Ü–Ķ–Ĺ—ā—Ä–ł—Ā–ł—ā–Ķ—ā, —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –į—Ā–ł–ľ–Ņ—ā–ĺ—ā –ł –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
¬†–ü—Ä–ł–≤–Ķ–ī–Ķ–ľ –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ļ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–ľ—É –≤–ł–ī—É, –ī–Ľ—Ź —ć—ā–ĺ–≥–ĺ –≤—č–ī–Ķ–Ľ–ł–ľ –Ņ–ĺ–Ľ–Ĺ—č–Ķ –ļ–≤–į–ī—Ä–į—ā—č:¬†
$$16x^2-9y^2-64x-54y-161=(16x^2-64x)-(9y^2+54y)-161=$$
$$16(x^2-4x+4-4)-9(y^2+6y+9-9)-161=16(x-2)^2-64-9(y+3)^2+81-161=$$
$$16(x-2)^2-9(y+3)^2-144=0\Rightarrow16(x-2)^2-9(y+3)^2=144|:144\Rightarrow$$
$$ \frac{(x-2)^2}{9}-\frac{(y+3)^2}{16}=1\Rightarrow\frac{(x-2)^2}{9}-\frac{(y+3)^2}{16}=1.$$
–≠—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č. –¶–Ķ–Ĺ—ā—Ä –ł–ľ–Ķ–Ķ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $C=(x_0, y_0)=(2,-3);$ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł $a=3,$ $b=4.$
$c=\sqrt{a^2+b^2}\Rightarrow c=\sqrt{9+16}=\sqrt {25}=5\Rightarrow e=\frac{c}{a}=\frac{5}{3}.$
 
–ź—Ā–ł–ľ–Ņ—ā–ĺ—ā—č –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č c —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$y=\pm\frac{b}{a}x,$ –į —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ¬†$C=(x_0, y_0) -$ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ¬†$y-y_0=\pm\frac{b}{a}(x-x_0),$
 $$y+3=\frac{4}{3}(x-2)\Rightarrow 3y+9=4x-8\Rightarrow 4x-3y-17=0.$$
 $$y+3=-\frac{4}{3}(x-2)\Rightarrow 3y+9=-4x+8\Rightarrow 4x+3y+1=0.$$
 
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā –ī–Ľ—Ź —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
¬†$D_1: x=-\frac{3}{5/3}=-\frac{9}{5} $ –ł $D_2: x=\frac{3}{5/3}=\frac{9}{5}.$ –ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —É –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —ć–Ľ–Ľ–ł–Ņ—Ā–į —Ü–Ķ–Ĺ—ā—Ä —Ā–ľ–Ķ—Č–Ķ–Ĺ, —ā–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā—Ā—č –Ī—É–ī—É—ā –ł–ľ–Ķ—ā—Ć —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź¬†$D_1: x=x_0-a/e$ –ł $D_2: x=x_0+a/e:$
 $$D_1: x=2-\frac{9}{5}=\frac{10-9}{5}=\frac{1}{5}\Rightarrow 5x-1=0 $$  
$$D_2: x=2+\frac{9}{5}=\frac{10+9}{5}=\frac{19}{5}\Rightarrow 5x-19=0 $$
–ě—ā–≤–Ķ—ā:¬†$C=(2, -3);$ ¬†$a=3,$ $b=4;$¬†$ e=\frac{5}{3},$¬†$4x-3y-17=0,$ $4x+3y+1=0,$¬†$D_1:5x-1=0, $ $D_2: 5x-19=0.$
 
2.272.¬†–£–Ī–Ķ–ī–ł–≤—ą–ł—Ā—Ć, —á—ā–ĺ —ā–ĺ—á–ļ–į $M(-5, 9/4)$ –Ľ–Ķ–∂–ł—ā –Ĺ–į –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–Ķ $\frac{x^2}{16}-\frac{y^2}{9}=1,$ –Ĺ–į–Ļ—ā–ł —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ķ —Ä–į–ī–ł—É—Ā—č —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł –ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ć—ā–ĺ–Ļ —ā–ĺ—á–ļ–ł –ī–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.¬†
–ü—Ä–ĺ–≤–Ķ—Ä–ł–ľ, —á—ā–ĺ –∑–į–ī–į–Ĺ–Ĺ–į—Ź —ā–ĺ—á–ļ–į –Ľ–Ķ–∂–ł—ā –Ĺ–į –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–Ķ:
$$\frac{x^2}{16}-\frac{y^2}{9}=1\Rightarrow \frac{(-5)^2}{16}-\frac{(9/4)^2}{9}=\frac{25}{16}-\frac{81}{16\cdot 9}=\frac{25\cdot 9-81}{144}=\frac{144}{144}=1.$$
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ,¬†—ā–ĺ—á–ļ–į $M(-5, 9/4)$ –Ľ–Ķ–∂–ł—ā –Ĺ–į –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ–Ķ $\frac{x^2}{16}-\frac{y^2}{9}=1.$
–Ē–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ķ —Ä–į–ī–ł—É—Ā—č, –Ĺ–į–Ļ–ī–Ķ–ľ —Ą–ĺ–ļ—É—Ā—č –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č:
$c=\sqrt{a^2+b^2}\Rightarrow c=\sqrt{16+9}=\sqrt {25}=5$ –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —Ą–ĺ–ļ—É—Ā—č –ł–ľ–Ķ—é—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $F_1(-5, 0), F_2(5, 0).$
–§–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ķ —Ä–į–ī–ł—É—Ā—č —ā–ĺ—á–ļ–ł, –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$r_1=|\overline{F_1M}|$ –ł¬†$r_2=|\overline{F_2M}|.$¬†
$$\overline{F_1M}=(-5-(-5), 9/4)=(0, 9/4)\Rightarrow |\overline{F_1M}=\sqrt{(9/4)^2}|=9/4.$$
$$\overline{F_2M}=(-5-5, 9/4)=(-10, 9/4)\Rightarrow |\overline{F_1M}=\sqrt{10^2+(9/4)^2}|=$$ $$=\sqrt{100+81/16}=\sqrt\frac{1681}{16}=\frac{41}{4}.$$
–ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł $M$ –ī–ĺ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā, –Ĺ–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā¬†–Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ¬†$D_1: x=-a/e$ –ł $D_2: x=a/e:$
$e=\frac{c}{a}=\frac{5}{4};$
$D_1: x=-\frac{4}{5/4}\Rightarrow x=-\frac{16}{5}\Rightarrow 5x+16=0;$
$D_2: x=\frac{4}{5/4}\Rightarrow x=\frac{16}{5}\Rightarrow 5x-16=0;$
–†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $P(x_0, y_0)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ $L: Ax+By+C=0$¬†–≤—č—á–ł—Ā–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $M(5, 9/4)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ¬†$D_1: \sqrt 5x+16=0$
$$d_1=\left|\frac{5\cdot 5+16}{\sqrt{5^2}}\right|=\frac{41}{5};$$
—Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ—ā —ā–ĺ—á–ļ–ł $M(5, 9/4)$ –ī–ĺ –Ņ—Ä—Ź–ľ–ĺ–Ļ¬†$D_2: \sqrt 5x-16=0$
$$d_2=\left|\frac{5\cdot 5-16}{\sqrt{5^2}}\right|=\frac{9}{5}.$$
–ě—ā–≤–Ķ—ā:¬†$r_1=9/4,$¬†$r_2=\frac{41}{4};$¬†$d_1=\frac{41}{5};$¬†$d_2=\frac{9}{5}.$¬†
 
2.273.¬†–Ě–į–Ļ—ā–ł —ā–ĺ—á–ļ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č $\frac{x^2}{9}-\frac{y^2}{16}=1,$ –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–Ķ—Ā—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł $7$ –ĺ—ā —Ą–ĺ–ļ—É—Ā–į $F_1.$
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ė–∑ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–ĺ–Ľ—É–ĺ—Ā–ł: $a=3, \, b=4.$ –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ,¬†$c=\sqrt{a^2+b^2}\Rightarrow c=\sqrt{9+16}=\sqrt {25}=5.$
–ě—ā—Ā—é–ī–į –Ĺ–į—Ö–ĺ–ī–ł–ľ $F_1=(-5, 0).$
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ľ–Ķ—Ā—ā–ĺ —ā–ĺ—á–Ķ–ļ, —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č—Ö –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł¬†$7$ –ĺ—ā —Ą–ĺ–ļ—É—Ā–į $F_1,$ —ć—ā–ĺ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ¬†$F_1=(-5, 0)$ –ł —Ä–į–ī–ł—É—Ā–ĺ–ľ $r=7:$
$$(x+5)^2+y^2=7^2.$$
–ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —ā–ĺ—á–ļ–ł –≥–ł–Ņ–Ķ—Ä–Ī–ĺ–Ľ—č $\frac{x^2}{9}-\frac{y^2}{16}=1,$ –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–Ķ—Ā—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł $7$ –ĺ—ā —Ą–ĺ–ļ—É—Ā–į $F_1,$ —Ä–Ķ—ą–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ—É —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ
$$\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{y^2}{16}=1\\(x+5)^2+y^2=7^2\end{array}\right.$$ 
$$\Rightarrow\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{y^2}{16}=1\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}\frac{x^2}{9}-\frac{7^2-(x+5)^2}{16}=1\\y^2=7^2-(x+5)^2\end{array}\right.$$ 
$$\Rightarrow\left\{\begin{array}{lcl}16x^2-9(49-x^2-10x-25)=144\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}16x^2-216+9x^2+90x=144\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow$$ 
$$\Rightarrow\left\{\begin{array}{lcl}25x^2+90x-360=0\\y^2=7^2-(x+5)^2\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}5x^2+18x-72=0\\y^2=7^2-(x+5)^2\end{array}\right.$$
–†–Ķ—ą–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ¬†$5x^2+18x-72=0:$
$D=18^2+4\cdot5\cdot72=324+1440=1764=42^2.$
$x_1=\frac{-18+42}{10}=\frac{24}{10}=2,4;$   $x_2=\frac{-18-42}{10}=-6.$
–Ě–į—Ö–ĺ–ī–ł–ľ¬†—Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $y:$ $y_1=\pm\sqrt{24-2,4^2-10\cdot 2,4}=\sqrt{-5,76}$¬†- –Ĺ–Ķ—ā –ļ–ĺ—Ä–Ĺ–Ķ–Ļ. ¬†
$y_2=\pm\sqrt{24-6^2+10\cdot5}=\pm4\sqrt{3}.$
–ě—ā–≤–Ķ—ā: $(-6, \pm4\sqrt 3).$
 
–ü–į—Ä–į–Ī–ĺ–Ľ–į.
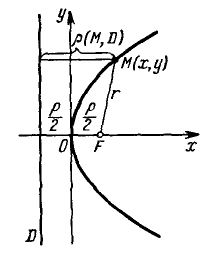
–ü–į—Ä–į–Ī–ĺ–Ľ–į —Ā –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ $y^2=2px, p>0,$ –ł–ľ–Ķ–Ķ—ā —Ą–ĺ—Ä–ľ—ɬ†–ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–Ĺ—É—é –Ĺ–į¬†—Ä–ł—Ā—É–Ĺ–ļ–Ķ.
–ß–ł—Ā–Ľ–ĺ $p$ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–ľ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č. –Ę–ĺ—á–ļ–į¬†$O -$ –Ķ–Ķ –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ, –į –ĺ—Ā—Ƭ†$Ox$ ¬†¬†- –ĺ—Ā—Ć—é –Ņ–į—Ä–į–Ī–ĺ–Ľ—č.
–Ę–ĺ—á–ļ–į $F\left(\frac{p}{2}, 0\right)$ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź —Ą–ĺ–ļ—É—Ā–ĺ–ľ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č, –≤–Ķ–ļ—ā–ĺ—Ä $\overline{FM} -$ ¬†—Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ —Ä–į–ī–ł—É—Ā-–≤–Ķ–ļ—ā–ĺ—Ä–į–ľ, ¬†–į —á–ł—Ā–Ľ–ĺ $r=|\overline{FM}| -$ ¬†—Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ —Ä–į–ī–ł—É—Ā–ĺ–ľ —ā–ĺ—á–ļ–ł $M,$ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—Č–Ķ–Ļ –Ņ–į—Ä–į–Ī–ĺ–Ľ–Ķ.¬†
–ü—Ä—Ź–ľ–į—Ź $D: x=-p/2$ –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į—Ź –ĺ—Ā–ł –ł –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź –Ĺ–į —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł–ł $p/2$ –ĺ—ā –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ–į—Ä–į–Ī–ĺ–Ľ—č, –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ķ–Ķ –ī–ł—Ä–Ķ–ļ—ā—Ä–ł—Ā–ĺ–Ļ.¬†
 
–ü—Ä–ł–ľ–Ķ—Ä—č.
2.285 (–į). –ü–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –Ņ–į—Ä–į–Ī–ĺ–Ľ—É $y^2=6x$ –ł –Ĺ–į–Ļ—ā–ł –Ķ–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä—č.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü–į—Ä–į–ľ–Ķ—ā—Ä $p$ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č –ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ—ā–ł –ł–∑ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź¬†$y^2=2px: $
$$y^2=6x\Rightarrow y^2=2\cdot 3x\Rightarrow p=2.$$
–°–ī–Ķ–Ľ–į–Ķ–ľ —Ä–ł—Ā—É–Ĺ–ĺ–ļ:
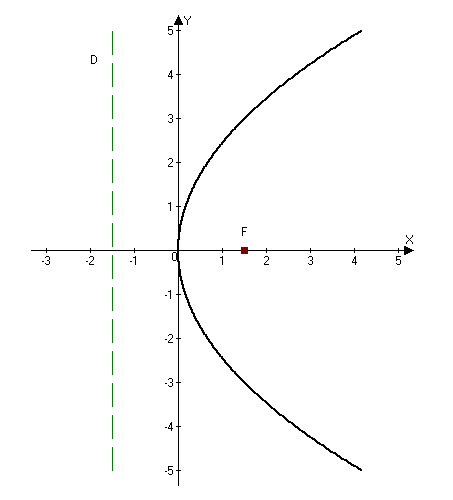
–ě—ā–≤–Ķ—ā: $p=3.$
  {jumi[*4]}
2.286 (–į). –Ě–į–Ņ–ł—Ā–į—ā—Ć —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č —Ā –≤–Ķ—Ä—ą–ł–Ĺ–ĺ–Ļ –≤ –Ĺ–į—á–į–Ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā, –Ķ—Ā–Ľ–ł –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ –Ņ–į—Ä–į–Ī–ĺ–Ľ–į —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–į –≤ –Ľ–Ķ–≤–ĺ–Ļ –Ņ–ĺ–Ľ—É–Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ—Ā–ł $Ox$ –ł $p=1/2.$
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—ɬ†–Ņ–į—Ä–į–Ī–ĺ–Ľ–į —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–į –≤ –Ľ–Ķ–≤–ĺ–Ļ –Ņ–ĺ–Ľ—É–Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł, —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ—Ā–ł $Ox,$ —ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č –Ī—É–ī–Ķ—ā –ł–ľ–Ķ—ā—Ć –≤–ł–ī $y^2=-2px.$ –ü–ĺ–ī—Ā—ā–į–≤–Ľ—Ź—Ź –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į, –Ĺ–į—Ö–ĺ–ī–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č:
$$y^2=-2\cdot\frac{1}{2}x=-x.$$
–ě—ā–≤–Ķ—ā: $y^2=-x.$
 
2.288 (–į). –£—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć, —á—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ $y^2=4x-8$ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā –Ņ–į—Ä–į–Ī–ĺ–Ľ—É, –Ĺ–į–Ļ—ā–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č –Ķ–Ķ –≤–Ķ—Ä—ą–ł–Ĺ—č $A$ –ł –≤–Ķ–Ľ–ł—á–ł–Ĺ—É –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–į $p.$
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č, —Ü–Ķ–Ĺ—ā—Ä –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ā–ī–≤–ł–Ĺ—É—ā –≤ —ā–ĺ—á–ļ—É ¬†$(x_0, y_0),$ –ł–ľ–Ķ–Ķ—ā –≤–ł–ī $(y-y_0)^2=2p(x-x_0)^2.$¬†
–ü—Ä–ł–≤–Ķ–ī–Ķ–ľ –∑–į–ī–į–Ĺ–Ĺ–ĺ–Ķ —É—Ä–į–≤–Ĺ–Ĺ–ł–Ķ –ļ —ā–į–ļ–ĺ–ľ—É –≤–ł–ī—É:
$y^2=4(x-2).$
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, $y^2=4(x^2-2)$ - –Ņ–į—Ä–į–Ī–ĺ–Ľ–į —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤ —ā–ĺ—á–ļ–Ķ $(0, 2).$ –ü–į—Ä–į–ľ–Ķ—ā—Ä $p=2.$
–ě—ā–≤–Ķ—ā: $C(0, 2),$ $p=2.$ ¬†
 
2.290. –í—č—á–ł—Ā–Ľ–ł—ā—Ć —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä —ā–ĺ—á–ļ–ł $M$ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č $y^2=12x,$ –Ķ—Ā–Ľ–ł $y(M)=6.$
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä —ā–ĺ—á–ļ–ł $M,$ –Ĺ–į–Ļ–ī–Ķ–ľ –Ķ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č. –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –Ņ–ĺ–ī—Ā—ā–į–≤–ł–ľ –≤ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ–į—Ä–į–Ī–ĺ–Ľ—č –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—É $y:$ $$6^2=12x\Rightarrow 36=12x\Rightarrow x=3.$$¬†
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —ā–ĺ—á–ļ–į $M$ –ł–ľ–Ķ–Ķ—ā¬†–ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $(3, 6).$
–ė–∑ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–į—Ä–į–Ī–ĺ–Ľ—č $y^2=12x$ –Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä –Ņ–į—Ä–į–Ī–ĺ–Ľ—č: $y^2=2\cdot 6x\Rightarrow p=6.$ –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ą–ĺ–ļ—É—Ā –Ņ–į—Ä–į–Ī–ĺ–Ľ—č –ł–ľ–Ķ–Ķ—ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č $F(3, 0).$
–Ē–į–Ľ–Ķ–Ķ –Ĺ–į—Ö–ĺ–ī–ł–ľ —Ą–ĺ–ļ–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä —ā–ĺ—á–ļ–ł:
$r=|FM|=\sqrt{(3-3)^2+(6-0)^2}=6.$
–ě—ā–≤–Ķ—ā: $6.$
 
2.298. –ė–∑ —Ą–ĺ–ļ—É—Ā–į –Ņ–į—Ä–į–Ī–ĺ–Ľ—č $y^2=12x$ –Ņ–ĺ–ī –ĺ—Ā—ā—Ä—č–ľ —É–≥–Ľ–ĺ–ľ $\alpha$ –ļ –ĺ—Ā–ł $Ox$ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ –Ľ—É—á —Ā–≤–Ķ—ā–į, ¬†–Ņ—Ä–ł—á–Ķ–ľ¬†$tg\alpha=\frac{3}{4}.$¬†–Ě–į–Ņ–ł—Ā–į—ā—Ć —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ľ–Ķ–∂–ł—ā –Ľ—É—á, –ĺ—ā—Ä–į–∂–Ķ–Ĺ–Ĺ—č–Ļ –ĺ—ā –Ņ–į—Ä–į–Ī–ĺ–Ľ—č.
–†–Ķ—ą–Ķ–Ĺ–ł–Ķ.
–Ě–į–Ļ–ī–Ķ–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ą–ĺ–ļ—É—Ā–į. –ė–∑ –ļ–į–Ĺ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –Ņ–į—Ä–į–Ī–ĺ–Ľ—謆$y^2=2px$¬†–Ĺ–į—Ö–ĺ–ī–ł–ľ –Ņ–į—Ä–į–ľ–Ķ—ā—Ä: $y^2=12x=2\cdot 6x\Rightarrow p=6.$
–ö–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —Ą–ĺ–ļ—É—Ā–į $F(p/2, 0)\Rightarrow F(3,0).$
–Ē–į–Ľ–Ķ–Ķ –Ĺ–į—Ö–ĺ–ī–ł–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä–į—Ź –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É $(3, 0)$ –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ $\alpha: tg\alpha=\frac{3}{4}$ –ļ –ĺ—Ā–ł $OX.$ –£—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ł—Č–Ķ–ľ –≤ –≤–ł–ī–Ķ $y=kx+b,$ –≥–ī–Ķ $k=tg\alpha=\frac{3}{4}.$
$y=\frac{3}{4}x+b$
–ß—ā–ĺ–Ī—č –Ĺ–į–Ļ—ā–ł $b,$ –≤ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä—Ź–ľ–ĺ–Ļ –Ņ–ĺ–ī—Ā—ā–į–≤–ł–ľ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—č —ā–ĺ—á–ļ–ł $(3, 0):$
$0=\frac{3}{4}\cdot 3+b\Rightarrow b=-\frac{9}{4}.$ –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ľ—É—á–į, –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –ł–∑ —Ą–ĺ–ļ—É—Ā–į $y=\frac{3}{4}x-\frac{9}{4}.$
–Ē–į–Ľ–Ķ–Ķ, –Ĺ–į–Ļ–ī–Ķ–ľ —ā–ĺ—á–ļ—É –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–į–Ļ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ —Ā –Ņ–į—Ä–į–Ī–ĺ–Ľ–ĺ–Ļ:
$$\left\{\begin{array}{lcl}y=\frac{3}{4}x-\frac{9}{4}\\y^2=12x\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}3x-4y-9=0\\x=\frac{y^2}{12}\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}\frac{3y^2}{12}-4y-9=0\\x=\frac{y^2}{12}\end{array}\right.\Rightarrow$$ $$\left\{\begin{array}{lcl}y^2-16y-36=0\\x=\frac{y^2}{12}\end{array}\right.$$
$$y^2-16y-36=0$$
$$D=256+4\cdot1\cdot36=256+144=400.$$
$$y_1=\frac{16+20}{2}=18\qquad y_2=\frac{16-20}{2}=-2.$$
–ü–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ–ĺ —É—Ā–Ľ–ĺ–≤–ł—é –Ľ—É—á –Ņ–į–ī–į–Ķ—ā –Ņ–ĺ–ī –ĺ—Ā—ā—Ä—č–ľ —É–≥–Ľ–ĺ–ľ, —ā–ĺ –ľ—č —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ —ā–ĺ–Ľ—Ć–ļ–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā—É $y=18.$ –°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ $x=\frac{18^2}{12}=\frac{324}{12}=27.$
–Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ľ—É—á –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā –Ņ–į—Ä–į–Ī–ĺ–Ľ—É –≤ —ā–ĺ—á–ļ–Ķ $(27, 18).$
–Ē–į–Ľ–Ķ–Ķ –Ĺ–į–Ļ–ī–Ķ–ľ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ļ –Ņ–į—Ä–į–Ī–ĺ–Ľ–Ķ –≤ –Ĺ–į–Ļ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā–ĺ—á–ļ–Ķ $(27, 18)$ –Ņ–ĺ ¬†—Ą–ĺ—Ä–ľ—É–Ľ–Ķ¬†$(y-y_0)=y'(x_0)(x-x_0):$
$$y=\sqrt{12x}\Rightarrow y'=\sqrt {12}\frac{1}{2\sqrt x}=\frac{\sqrt 3}{\sqrt{x}}\Rightarrow$$
$$\Rightarrow y'(27)=\frac{\sqrt 3}{\sqrt{ 27}}=\frac{1}{3}.$$
$$y(27)=18.$$
–ü–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ –≤—Ā–Ķ –Ĺ–į–Ļ–ī–Ķ–Ĺ–Ĺ—č–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –≤ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ:
$y-18=\frac{1}{3}(x-27)\Rightarrow 3y-54=x-27\Rightarrow x-3y+27=0.$
–Ē–į–Ľ–Ķ–Ķ, –Ĺ–į–Ļ–ī–Ķ–ľ —É–≥–ĺ–Ľ $\beta$ –ľ–Ķ–∂–ī—É –Ľ—É—á–Ķ–ľ¬†$y=\frac{3}{4}x-\frac{9}{4}$¬†¬†–ł –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ¬†$x-3y+27=0.$ –Ē–Ľ—Ź —ć—ā–ĺ–≥–ĺ –ĺ–Ī–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –∑–į–Ņ–ł—ą–Ķ–ľ –≤ –≤–ł–ī–Ķ $y=k_1x+b_1$ ¬†–ł $y=k_2+b_2$ —É–≥–ĺ–Ľ –≤—č—á–ł—Ā–Ľ–ł–ľ –Ņ–ĺ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ $tg(L_1, L_2)=\frac{k_1-k_2}{1+k_1\cdot k_2}$
$$L_1: y=\frac{3}{4}x-\frac{9}{4}\Rightarrow k_1=\frac{3}{4};$$
$$L_2: x-3y+27=0\Rightarrow y=\frac{1}{3}x+9\Rightarrow k_2=\frac{1}{3}.$$
$$tg \beta=tg(L_1, L_2)=\frac{\frac{3}{4}-\frac{1}{3}}{1+\frac{3}{4}\frac{1}{3}}=\frac{\frac{5}{12}}{\frac{5}{4}}=\frac{1}{3}.$$
–õ–Ķ–≥–ļ–ĺ —É–≤–ł–ī–Ķ—ā—Ć, —á—ā–ĺ —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –Ľ—É—á–Ķ–ľ $L_1,$ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–Ĺ—č–ľ –ł–∑ —Ą–ĺ–ļ—É—Ā–į –ł –Ķ–≥–ĺ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ —Ä–į–≤–Ķ–Ĺ $\pi-2\beta,$ –į —É–≥–ĺ–Ľ –ľ–Ķ–∂–ī—É –ĺ—ā—Ä–į–∂–Ķ–Ĺ–Ĺ—č–ľ –Ľ—É—á–Ķ–ľ –ł –ĺ—Ā—Ć—é $Ox$ $\pi-(\pi-2\beta)-\alpha=2\beta-\alpha.$¬†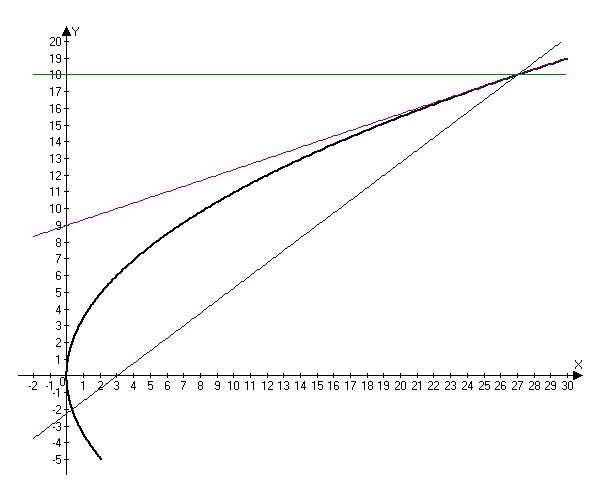
–ó–Ĺ–į—Ź $tg\beta=\frac{1}{3}$ –ł $tg\alpha=k_1=\frac{3}{4}$ –ł –≤—Ā–Ņ–ĺ–ľ–ł–Ĺ–į—Ź —Ą–ĺ—Ä–ľ—É–Ľ—č –ī–Ľ—Ź –ī–≤–ĺ–Ļ–Ĺ–ĺ–≥–ĺ —É–≥–Ľ–į —ā–į–Ĺ–≥–Ķ–Ĺ—Ā–į –ł —ā–į–Ĺ–≥–Ķ–Ĺ—Ā —Ä–į–∑–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į—Ö–ĺ–ī–ł–ľ $tg(2\beta-\alpha):$
$$tg 2\beta=\frac{2tg\beta}{1-tg^2\beta}=\frac{\frac{2}{3}}{1-\frac{1}{9}}=\frac{\frac{2}{3}}{\frac{8}{9}}=\frac{3}{4}.$$
$$tg(2\beta-\alpha)=\frac{tg2\beta-tg\alpha}{1+tg2\beta tg\alpha}=\frac{\frac{3}{4}-\frac{3}{4}}{1+\frac{3}{4}\frac{3}{4}}=0.$$ –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ—Ä—Ź–ľ–į—Ź, —Ā–ĺ–ī–Ķ—Ä–∂–į—Č–į—Ź –ĺ—ā—Ä–į–∂–Ķ–Ĺ–Ĺ—č–Ļ –Ľ—É—á –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–į –ĺ—Ā–ł $Ox.$ –Ę–į–ļ –ļ–į–ļ –ĺ–Ĺ–į –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É $(27, 18),$ —ā–ĺ –ľ–ĺ–∂–Ĺ–ĺ –∑–į–Ņ–ł—Ā–į—ā—Ć –Ķ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ $y=18.$
–ě—ā–≤–Ķ—ā: $y=18.$¬†
 
 
 


