–Θ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α, –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄, –Ω–Α―Ä–Α–±–Ψ–Μ―΄ –≤ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―².
 
–¦–Η―²–Β―Ä–Α―²―É―Ä–Α: –Γ–±–Ψ―Ä–Ϋ–Η–Κ –Ζ–Α–¥–Α―΅ –Ω–Ψ –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Β. –ß–Α―¹―²―¨ 1. –ü–Ψ–¥ ―Ä–Β–¥ –ê. –£. –ï―³–Η–Φ–Ψ–≤–Α, –ë. –ü. –î–Β–Φ–Η–¥–Ψ–≤–Η―΅–Α.
–ü―Ä–Η–Φ–Β―Ä.
–ü―É―¹―²―¨ $\Gamma -$ ―ç–Μ–Μ–Η–Ω―¹, –≤–Β―²–≤―¨ –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ –Η–Μ–Η –Ω–Α―Ä–Α–±–Ψ–Μ–Α, $F -$ ―³–Ψ–Κ―É―¹ ―ç―²–Ψ–Ι –Κ―Ä–Η–≤–Ψ–Ι, $D -$ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤―É―é―â–Α―è –¥–Η―Ä–Β–Κ―²―Ä–Η―¹–Α. –£―΄–≤–Β―¹―²–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Κ―Ä–Η–≤–Ψ–Ι $\Gamma$ –≤ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―², –Ω–Ψ–Μ―é―¹ –Κ–Ψ―²–Ψ―Ä–Ψ–Ι ―¹–Ψ–≤–Ω–Α–¥–Α–Β―² ―¹ ―³–Ψ–Κ―É―¹–Ψ–Φ –Α –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é –Κ―Ä–Η–≤–Ψ–Ι (―¹–Φ ¬†―Ä–Η―¹―É–Ϋ–Ψ–Κ 1).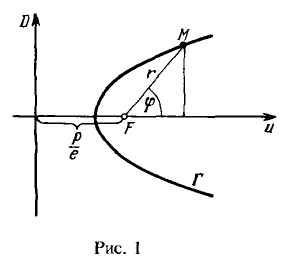
–†–Β―à–Β–Ϋ–Η–Β.
–û–±―â–Β–Β ―¹–≤–Ψ–Ι―¹―²–≤–Ψ ―ç–Μ–Μ–Η–Ω―¹–Α, –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ –Η –Ω–Α―Ä–Α–±–Ψ–Μ―΄ ―¹–Ψ―¹―²–Ψ–Η―² –≤ ―¹–Μ–Β–¥―É―é―â–Β–Φ¬†$$M\in\Gamma\Leftrightarrow\frac{\rho(M, F)}{\rho(M, D)}=const=e,\qquad\qquad (1)$$–≥–¥–Β $e -$ ―ç–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―² –Κ―Ä–Η–≤–Ψ–Ι ( $e<1$ –¥–Μ―è ―ç–Μ–Μ–Η–Ω―¹–Α, $e>1$ –¥–Μ―è –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ –Η $e=1$ –¥–Μ―è –Ω–Α―Ä–Α–±–Ψ–Μ―΄)
–û–±–Ψ–Ζ–Ϋ–Α―΅–Η–Φ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―³–Ψ–Κ―É―¹―΄ –¥–Ψ –¥–Η―Ä–Β–Κ―²―Ä–Η―¹―΄ ―΅–Β―Ä–Β–Ζ $\frac{p}{e}$( $p-$ –Ω–Α―Ä–Α–Φ–Β―²―Ä –Κ―Ä–Η–≤–Ψ–Ι, –Ϋ–Α–Ζ―΄–≤–Α–Β–Φ―΄–Ι –Ω–Ψ–Μ―É―³–Ψ–Κ–Α–Μ―¨–Ϋ―΄–Φ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Ψ–Φ). –Δ–Ψ–≥–¥–Α –Η–Ζ ―Ä–Η―¹―É–Ϋ–Κ–Α 1 ―¹–Μ–Β–¥―É–Β―², ―΅―²–Ψ $\rho(M, F)=r$ –Η $\rho(M, D)=\frac{p}{e}+r\cos\varphi.$ –ü–Ψ–¥―¹―²–Α–≤–Μ―è―è ―ç―²–Η –≤―΄―Ä–Α–Ε–Β–Ϋ–Η―è –≤ (1), –Ω–Ψ–Μ―É―΅–Α–Β–Φ $$\frac{r}{\frac{p}{e}+r\cos\varphi}=e,$$ –Ψ―²–Κ―É–¥–Α $$r=\frac{p}{1-e\cos\varphi}.\qquad\qquad (2)$$ –Θ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β (2) –Η –Β―¹―²―¨ –Η―¹–Κ–Ψ–Φ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –≤ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Ι ―¹–Η―¹―²–Β–Φ–Β –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―², –Ψ–±―â–Β–Β –¥–Μ―è ―ç–Μ–Μ–Η–Ω―¹–Α, –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ –Η –Ω–Α―Ä–Α–±–Ψ–Μ―΄.
–ü―Ä–Η–Φ–Β―Ä―΄.
2.321(–Α).
–î–Μ―è ―ç–Μ–Μ–Η–Ω―¹–Α $\frac{x^2}{25}+\frac{y^2}{16}=1$ –Ϋ–Α–Ω–Η―¹–Α―²―¨ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β, ―¹―΅–Η―²–Α―è, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é –Α–±―¹―Ü–Η―¹―¹, –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ –Μ–Β–≤–Ψ–Φ ―³–Ψ–Κ―É―¹–Β.¬†
–†–Β―à–Β–Ϋ–Η–Β.
–ù–Α–Ι–¥–Β–Φ ―ç–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―² –Ω–Α―Ä–Α–±–Ψ–Μ―΄ –Η –Ω–Α―Ä–Α–Φ–Β―²―Ä $p:$
$a=5,$ $b=4,$ $c=\sqrt{a^2-b^2}=\sqrt{25-16}=3.$
$e=\frac{c}{a}=\frac{3}{5}.$
–†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―³–Ψ–Κ―É―¹–Α –¥–Ψ –¥–Η―Ä–Β–Κ―²―Ä–Η―¹―΄ $\frac{p}{e}=\frac{a}{e}-c\Rightarrow p=e\left(\frac{a}{e}-c\right)\Rightarrow p=\frac{3}{5}\left(\frac{5}{\frac{3}{5}-3}\right)=\frac{3}{5}\cdot\frac{25-9}{3}=\frac{16}{5}.$
–î–Α–Μ–Β–Β, –Ω–Ψ–¥―¹―²–Α–≤–Μ―è―è –Ϋ–Α–Ι–¥–Β–Ϋ–Ϋ―΄–Β –Ω–Α―Ä–Α–Φ–Β―²―Ä―΄ –≤ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β (2), –Ϋ–Α–Ι–¥–Β–Ϋ–Ϋ–Ψ–Β –≤ –Ω―Ä–Β–¥―΄–¥―É―â–Β–Ι –Ζ–Α–¥–Α―΅–Β, –Ϋ–Α–Ι–¥–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –¥–Α–Ϋ–Ϋ–Ψ–≥–Ψ ―ç–Μ–Μ–Η–Ω―¹–Α:
$$r=\frac{\frac{16}{5}}{1-\frac{3}{5}\cos\varphi}=\frac{16}{5-3\cos\varphi}.$$ 
–û―²–≤–Β―²:¬†$r=\frac{16}{5-3\cos\varphi}.$¬†
 {jumi[*4]}
 
2.324(–Α).
–ù–Α–Ω–Η―¹–Α―²―¨ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Κ―Ä–Η–≤–Ψ–Ι –≤―²–Ψ―Ä–Ψ–≥–Ψ –Ω–Ψ―Ä―è–¥–Κ–Α $r=\frac{9}{5-4\cos\varphi}.$
–†–Β―à–Β–Ϋ–Η–Β.
–ü―Ä–Η–≤–Β–¥–Β–Φ –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β, –Κ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―é –≤–Η–¥–Α¬†$r=\frac{p}{1-e\cos\varphi}:$
$$r=\frac{9}{5-4\cos\varphi}=\frac{9}{5(1-\frac{4}{5}\cos\varphi)}=\frac{\frac{9}{5}}{1-\frac{4}{5}\cos\varphi}.$$
–û―²―¹―é–¥–Α –Η–Φ–Β–Β–Φ: $e=\frac{4}{5},$ $p=\frac{9}{5}.$ –ü–Ψ―¹–Κ–Ψ–Μ―¨–Κ―É $e<1,$ ―²–Ψ –¥–Α–Ϋ–Ϋ–Α―è –Κ―Ä–Η–≤–Α―è - ―ç–Μ–Μ–Η–Ω―¹.
–î–Α–Μ–Β–Β, –Ω–Ψ–¥―¹―²–Α–≤–Μ―è―è –≤―΄―Ä–Α–Ε–Β–Ϋ–Η―è ―ç–Κ―¹―Ü–Β–Ϋ―²―Ä–Η―¹–Η―²–Β―²–Α –Η –Ω–Α―Ä–Α–Φ–Β―²―Ä–Α –Ω–Ψ –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Η―é, –Ϋ–Α–¥–Β–Φ –Ω–Ψ–Μ―É–Ψ―¹–Η ―ç–Μ–Μ–Η–Ω―¹–Α:¬†
$$e=\frac{c}{a}=\frac{4}{5}\Rightarrow 5c=4a;$$
$$\frac{p}{e}=\frac{a}{e}-c\Rightarrow \frac{9}{4}=\frac{a}{4/5}-c=\frac{5a-4c}{4}\Rightarrow 9=5a-4c.$$
 
–†–Β―à–Η–Φ ―¹–Η―¹―²–Β–Φ―É ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι $$\left\{\begin{array}{lcl}5c=4a\\5a-4c=9\end{array}\right.\left\{\begin{array}{lcl}c=\frac{4}{5}a\\5a-\frac{16}{5}a=9\end{array}\right.\left\{\begin{array}{lcl}c=\frac{4}{5}a\\\frac{9}{5}a=9\end{array}\right.\left\{\begin{array}{lcl}c=4\\a=5\end{array}\right.\Rightarrow$$
$$b=\sqrt{a^2-c^2}=\sqrt{25-16}=3.$$ 
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ζ–Α–Ω–Η―à–Β–Φ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç–Μ–Μ–Η–Ω―¹–Α:
$$\frac{x^2}{25}+\frac{y^2}{9}=1.$$
–û―²–≤–Β―²:¬†$\frac{x^2}{25}+\frac{y^2}{9}=1.$
 
2.326.
–£―΄–≤–Β―¹―²–Η –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,$ –Ω―Ä–Η ―É―¹–Μ–Ψ–≤–Η–Η, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é $Ox,$ –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ ―Ü–Β–Ϋ―²―Ä–Β –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄.
–†–Β―à–Β–Ϋ–Η–Β.
–Δ–Α–Κ –Κ–Α–Κ –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ ―Ü–Β–Ϋ―²―Ä–Β –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄, ―²–Ψ $OM=r,$ ―²–Ψ–≥–¥–Α $\rho(M, D)=r\cos\varphi-\frac{a}{e},$ $\rho(M, F)=\sqrt {(r\sin\varphi)^2+(c-r\cos\varphi)^2}.$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Η–Ζ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è (1) –Ϋ–Α―Ö–Ψ–¥–Η–Φ:
$$M\in\Gamma\Leftrightarrow\frac{\rho(M, F)}{\rho(M, D)}=const=e\Rightarrow\frac{\sqrt{(r\sin\varphi)^2+(c-r\cos\varphi)^2}}{r\cos\varphi-\frac{a}{e}}=e\Rightarrow$$
$$\Rightarrow\frac{\sqrt{r^2+c^2-2rc\cos\varphi}}{r\cos\varphi-\frac{a}{e}}=e\Rightarrow $$
$$\Rightarrow r^2+c^2-2rc\cos\varphi=(er\cos\varphi-a)^2\Rightarrow$$
$$\Rightarrow r^2+c^2-2rc\cos\varphi=e^2r^2\cos^2\varphi-2er\cos\varphi+a^2\Rightarrow$$
$$\Rightarrow r^2(1-e^2\cos^2\varphi)-2rc\cos\varphi+2rc\cos\varphi=a^2-c^2=-b^2\Rightarrow$$
$$\Rightarrow r^2=\frac{b^2}{1-e^2\cos^2\varphi}.$$
–û―²–≤–Β―²:¬†$\Rightarrow r^2=\frac{b^2}{1-e^2\cos^2\varphi}.$
–î–Ψ–Φ–Α―à–Ϋ–Β–Β –Ζ–Α–¥–Α–Ϋ–Η–Β.
2.321(–±)¬†–î–Μ―è ―ç–Μ–Μ–Η–Ω―¹–Α $\frac{x^2}{25}+\frac{y^2}{16}=1$ –Ϋ–Α–Ω–Η―¹–Α―²―¨ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β, ―¹―΅–Η―²–Α―è, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é –Α–±―¹―Ü–Η―¹―¹, –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ –Ω―Ä–Α–≤–Ψ–Φ ―³–Ψ–Κ―É―¹–Β.¬†
–û―²–≤–Β―²:¬†$r=\frac{16}{5+3\cos\varphi}.$¬†
 
 
2.322.¬†–î–Μ―è –Ω―Ä–Α–≤–Ψ–Ι –≤–Β―²–≤–Η –≥–Η–Ω–Β―Ä–±–Ψ–Μ―΄ $\frac{x^2}{16}-\frac{y^2}{9}=1$ –Ϋ–Α–Ω–Η―¹–Α―²―¨ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β, ―¹―΅–Η―²–Α―è, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é –Α–±―¹―Ü–Η―¹―¹, –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è
–Α) –≤ –Μ–Β–≤–Ψ–Φ ―³–Ψ–Κ―É―¹–Β, ¬† ¬† ¬† ¬†–±) –≤ –Ω―Ä–Α–≤–Ψ–Φ ―³–Ψ–Κ―É―¹–Β.¬†
–û―²–≤–Β―²: –Α)¬†$r=-\frac{9}{4-5\cos\varphi},$ ¬†–±)¬†$r=\frac{9}{4-5\cos\varphi}.$¬†
 
2.323.¬†–î–Μ―è –Ω–Α―Ä–Α–±–Ψ–Μ―΄ $y^2=6x$ –Ϋ–Α–Ω–Η―¹–Α―²―¨ –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β, ―¹―΅–Η―²–Α―è, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Α ―¹ –Ψ―¹―¨―é –Α–±―¹―Ü–Η―¹―¹, –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ ―³–Ψ–Κ―É―¹–Β –Ω–Α―Ä–Α–±–Ψ–Μ―΄.¬†
–û―²–≤–Β―²:¬†$r=\frac{3}{1-\cos\varphi}.$¬†
 
2.324 (–±, –≤)¬†–ù–Α–Ω–Η―¹–Α―²―¨ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Η–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è ―¹–Μ–Β–¥―É―é―â–Η―Ö –Κ―Ä–Η–≤―΄―Ö –≤―²–Ψ―Ä–Ψ–≥–Ψ –Ω–Ψ―Ä―è–¥–Κ–Α:
б) $r=\frac{9}{4-5\cos\varphi},$        в) $r=\frac{3}{1-\cos\varphi}.$
–û―²–≤–Β―²:¬†–Α)¬†$\frac{x^2}{16}-\frac{y^2}{9}=1,$¬† –±)¬†$y^2=6x.$
 
 
2.327.¬†–£―΄–≤–Β―¹―²–Η –Ω–Ψ–Μ―è―Ä–Ϋ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω–Α―Ä–Α–±–Ψ–Μ―΄ $y^2=2px$ –Ω―Ä–Η ―É―¹–Μ–Ψ–≤–Η–Η, ―΅―²–Ψ –Ω–Ψ–Μ―è―Ä–Ϋ–Α―è –Ψ―¹―¨ ―¹–Ψ–Ϋ–Α–Ω―Ä–Α–≤–Μ–Β–Ϋ–Ϋ–Α ―¹ –Ψ―¹―¨―é $Ox,$ –Α –Ω–Ψ–Μ―é―¹ –Ϋ–Α―Ö–Ψ–¥–Η―²―¹―è –≤ –≤–Β―Ä―à–Η–Ϋ–Β –Ω–Α―Ä–Α–±–Ψ–Μ―΄.
–û―²–≤–Β―²:¬†$r=\frac{2p\cos\varphi}{\sin^2\varphi}.$¬†
 
 
 
 
 
 


