–Т–µ–Ї—В–Њ—А–љ–Њ–µ –Є —Б–Љ–µ—И–∞–љ–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤.
–Т–µ–Ї—В–Њ—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤.¬†
–Ы–Є—В–µ—А–∞—В—Г—А–∞: –°–±–Њ—А–љ–Є–Ї –Ј–∞–і–∞—З –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –І–∞—Б—В—М 1. –Я–Њ–і —А–µ–і –Р. –Т. –Х—Д–Є–Љ–Њ–≤–∞, –С. –Я. –Ф–µ–Љ–Є–і–Њ–≤–Є—З–∞.
–£–њ–Њ—А—П–і–Њ—З–µ–љ–љ–∞—П —В—А–Њ–є–Ї–∞ –љ–µ–Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $e_1, e_2, e_3$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –њ—А–∞–≤–Њ–є, –µ—Б–ї–Є –љ–∞–±–ї—О–і–∞—В–µ–ї—О, –љ–∞—Е–Њ–і—П—Й–µ–Љ—Г—Б—П –≤–љ—Г—В—А–Є —Г–≥–ї–∞, –Њ–±—А–∞–Ј–Њ–≤–∞–љ–љ–Њ–≥–Њ —Н—В–Є–Љ–Є –≤–µ–Ї—В–Њ—А–∞–Љ–Є, –Ї—А–∞—В—З–∞–є—И–Є–µ –њ–Њ–≤–Њ—А–Њ—В—Л –Њ—В $e_1$ –Ї $e_2$ –Є –Њ—В $e_2$ –Ї $e_3$ –Ї–∞–ґ—Г—В—Б—П –њ—А–Њ–Є—Б—Е–Њ–і—П—Й–Є–Љ–Є –њ—А–Њ—В–Є–≤ —З–∞—Б–Њ–≤–Њ–є —Б—В—А–µ–ї–Ї–Є. –Т –њ—А–Њ—В–Є–≤–љ–Њ–Љ —Б–ї—Г—З–∞–µ —В—А–Њ–є–Ї–∞ $(e_1, e_2, e_3)$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –ї–µ–≤–Њ–є.¬†
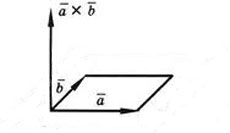
–Т–µ–Ї—В–Њ—А–љ—Л–Љ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ –≤–µ–Ї—В–Њ—А–∞ $a_1$ –љ–∞ –≤–µ–Ї—В–Њ—А $a_2$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –≤–µ–Ї—В–Њ—А, –Њ–±–Њ–Ј–љ–∞—З–∞–µ–Љ—Л–є —Б–Є–Љ–≤–Њ–ї–Њ–Љ $[a_1, a_2]$ (–Є–ї–Є $a_1\times a_2$) –Њ–њ—А–µ–і–µ–ї—П–µ–Љ—Л–є —Б–ї–µ–і—Г—О—Й–Є–Љ–Є —В—А–µ–Љ—П —Г—Б–ї–Њ–≤–Є—П–Љ–Є:
1) –і–ї–Є–љ–∞ –≤–µ–Ї—В–Њ—А–∞ $[a_1, a_2]$ —А–∞–≤–љ–∞ –њ–ї–Њ—Й–∞–і–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е $a_1$ –Є $a_2$ —В.–µ. $|[a_1, a_2]|=|a_1||a_2|\sin(\widehat{a_1, a_2})$
2) –≤–µ–Ї—В–Њ—А $[a_1, a_2]$ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –≤–µ–Ї—В–Њ—А–Њ–≤ $a_1$ –Є $a_2;$¬†
3) —Г–њ–Њ—А—П–і–Њ—З–µ–љ–љ–∞—П —В—А–Њ–є–Ї–∞ $a_1, a_2, [a_1, a_2]$ –њ—А–∞–≤–∞—П.
–Ш–Ј –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П —Б–ї–µ–і—Г–µ—В, —З—В–Њ $(\widehat{a_1,a_2})=\frac{\pi}{2}\Leftrightarrow [a_1, a_2]=0.$¬†
–Р–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П.
1) $[a_1, a_2]=-[a_2, a_1];$
2) $[\lambda a_1,a_2]=\lambda[a_1, a_2];$
3) $[a_1+a_2, b]=[a_1, b]+[a_2, b].$
–Х—Б–ї–Є $a_1(X_1, Y_1, Z_1) $ –Є $a_2(X_2, Y_2, Z_2) -$ –≤–µ–Ї—В–Њ—А—Л, –Ј–∞–і–∞–љ–љ—Л–µ —Б–≤–Њ–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –≤ –њ—А–∞–≤–Њ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ, —В–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П $[a_1, a_2]$ –≤ —В–Њ–Љ –ґ–µ –±–∞–Ј–Є—Б–µ –Є–Љ–µ–µ—В –≤–Є–і $$[a_1, a_2]=(Y_1Z_2-Z_1Y_2)i-(X_1Z_2-Z_1X_2)j+(X_1Y_2-Y_1X_2)k,$$ –Є–ї–Є, –≤ —Б–Є–Љ–≤–Њ–ї–Є—З–µ—Б–Ї–Њ–є –Ј–∞–њ–Є—Б–Є (—Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –њ–Њ–љ—П—В–Є—П –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—П 3-–≥–Њ –њ–Њ—А—П–і–Ї–∞) $$[a_1, a_2]=\begin{vmatrix}i& j& k\\X_1& Y_1&Z_1\\X_2&Y_2&Z_2\end{vmatrix}.$$
–Я—А–Є–Љ–µ—А—Л.
2.98. $|a_1|=1, |a_2|=2, (\widehat{a_1, a_2})=2\pi/3.$ –Т—Л—З–Є—Б–ї–Є—В—М:
–∞) $|[a_1, a_2]|$
–±) $|[2a_1+a_2, a_1+2a_2]|$
–≤) $|[a_1+3a_2, 3a_1-a_2]|.$
–†–µ—И–µ–љ–Є–µ.
а) $|[a_1, a_2]|=|a_1||a_2|\sin(\widehat{a_1, a_2})=2\sin({2\pi/3})=2\frac{\sqrt {3}}{2}=\sqrt 3.$
б) $[2a_1+a_2, a_1+2a_2]=[2a_1, a_1+2a_2]+[a_2, a_1+2a_2]=$
$=2[a_1, a_1+2a_2]+[a_2, a_1+2a_2]=-2[a_1+2a_2, a_1]-[a_1+2a_2, a_2]=$ 
$=-2[a_1, a_1]-2[2a_2, a_1]-[a_1, a_2]-[2a_2, a_2]=-4[a_2, a_1]-[a_1,a_2]=$
$=4[a_1, a_2]-[a_1, a_2]=3[a_1, a_2].$
$|[2a_1+a_2, a_1+2a_2]|=3|[a_1, a_2]|=3\sqrt 3.$
в) $[a_1+3a_2, 3a_1-a_2]=[a_1, 3a_1-a_2]+3[a_2, 3a_1-a_2]=$
$=-[3a_1-a_2, a_1]-3[3a_1-a_2, a_2]=$
$=-[3a_1, a_1]+[a_2, a_1]-9[a_1, a_2]+3[a_2, a_2]=-10[a_1, a_2].$
$|[a_1+3a_2, 3a_1-a_2]|=|10[a_1, a_2]|=10\sqrt 3.$
–Ю—В–≤–µ—В: –∞) $\sqrt 3;$ ¬†¬†¬† ¬† ¬† ¬† ¬† ¬†–±) $3\sqrt 3;$ ¬† ¬† ¬† ¬†¬† ¬† ¬† ¬†–≤) $10\sqrt 3.$
 
2.100. –£–њ—А–Њ—Б—В–Є—В—М –≤—Л—А–∞–ґ–µ–љ–Є—П:
–∞) $[i, j+k]-[j, i+k]+[k, i+j+k];$
–±) $[a+b+c, c]+[a+b+c, b]+[b-c,a];$
–≤) $[2a+b, c-a]+[b+c, a+b];$
–≥) $2i[j, k]+3j[i, k]+4k[i, j].$
–†–µ—И–µ–љ–Є–µ.
а) $[i, j+k]-[j, i+k]+[k, i+j+k]=-[j+k, i]+[i+k, j]-[i+j+k, k]=-[j, i]-[k, i]+[i, j]+[k, j]-[i, k]-[j, k]-[k, k]=$
$=[i, j]+[i, k]+[i, j]-[j, k]-[i, k]-[j, k]=2[i, j]-2[j, k]=$
$2\begin{vmatrix} i&j&k\\1&0&0\\0&1&0\end{vmatrix}-2\begin{vmatrix}i&j&k\\0&1&0\\0&0&1\end{vmatrix}=2k-2i.$ 
 
б) $[a+b+c, c]+[a+b+c, b]+[b-c,a]=$
$=[a,c]+[b, c]+[c, c]+[a, b]+ [b, b]+[c, b]+[b, a]-[c, a]=$
$=[a, c]+[b, c]+[a, b]-[b, c]-[a, b]+[a, c]=2[a, c].$
 
в) $[2a+b, c-a]+[b+c, a+b]=2[a, c-a]+[b,c-a]+[b, a+b]+[c, a+b]=$
$=-2[c-a, a]-[c-a, b]-[a+b, b]-[a+b, c]=$
$=-2[c, a]+2[a, a]-[c, b]+[a,b]-[a, b]-[b, b]-[a, c]-[b, c]=[a, c].$
–Ю—В–≤–µ—В: –∞) $2(k-i);$ ¬† ¬†–±) $2[a, c];$ ¬† ¬†–≤) $[a,c].$
 {jumi[*4]}
2.107. –Т—Л—З–Є—Б–ї–Є—В—М –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —Б –≤–µ—А—И–Є–љ–∞–Љ–Є $A(1, 1, 1), B(2, 3, 4)$ –Є $C(4, 3, 2).$
–†–µ—И–µ–љ–Є–µ.
$S \triangle ABC=\frac{1}{2}|[\overline{BA}, \overline{BC}]|.$
$\overline{BA}=(1-2; 1-3; 1-4)=(-1; -2; -3).$
$\overline{BC}=(4-2; 3-3; 2-4)=(2; 0; -2).$
$[\overline{BA}, \overline{BC}]=\begin{vmatrix}i&j&k\\-1&-2&-3\\2&0&-2\end{vmatrix}=4i-8j+4k.$
$S \triangle ABC=\frac{1}{2}|[\overline{BA}, \overline{BC}]|=\frac{1}{2}\sqrt{16+64+16}=\frac{\sqrt {96}}{2}=2\sqrt{6}.$
–Ю—В–≤–µ—В: $2\sqrt{6}.$
 
2.110. –Ф–ї—П –Ј–∞–і–∞–љ–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $a(2, 0, 3), b(-3, 5, 4), c(3, 4, -1)$ –≤—Л—З–Є—Б–ї–Є—В—М –њ—А–Њ–µ–Ї—Ж–Є—О –≤–µ–Ї—В–Њ—А–∞ $[a, b]$ –љ–∞ –≤–µ–Ї—В–Њ—А $(a, b)c.$
 
–†–µ—И–µ–љ–Є–µ.
–Э–∞–є–і–µ–Љ –≤–µ–Ї—В–Њ—А–∞ $d=[a, b]$ –Є $k=(a,b)c:$
$d=[a, b]=\begin{vmatrix}i&j&k\\2&0&3\\-3&5&4\end{vmatrix}=-15i-17j+10k=(-15, -17, 10);$
$k=(a, b)c=(-6+12)(3, 4, -1)=6(3, 4, -1)=(18, 24, -6).$
$Pr_k d=\frac{(d, k)}{|k|}=\frac{-270-408-60}{\sqrt{324+576+36}}=\frac{-738}{\sqrt {936}}=\frac{-738}{6\sqrt{26}}=\frac{-123}{\sqrt{26}}.$
–Ю—В–≤–µ—В: $\frac{-123}{\sqrt{26}}.$
 
2.112. –Э–∞–є—В–Є –≤–µ–Ї—В–Њ—А $[a, a+b]+[a, [a, b]],$ –µ—Б–ї–Є $a(2, 1, -3)$ $b(1, -1, 1).$
–†–µ—И–µ–љ–Є–µ.
$a+b=(2+1; 1-1; -3+1)=(3; 0; -2);$
$[a, a+b]=\begin{vmatrix}i&j&k\\2&1&-3\\3&0&-2\end{vmatrix}=-2i-5j-3k;$
$[a, b]=\begin{vmatrix}i&j&k\\2&1&-3\\1&-1&1\end{vmatrix}=-2i-5j-3k;$
$[a, [a, b]]=\begin{vmatrix}i&j&k\\2&1&-3\\-2&-5&-3\end{vmatrix}=-18i+12j-8k;$
$[a, a+b]+[a, [a, b]]=(-2; -5; -3)+(-18; 12; -8)=(-20; 7; -11).$
–Ю—В–≤–µ—В: $(-20; 7; -11).$
 
 
–°–Љ–µ—И–∞–љ–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤.
–°–Љ–µ—И–∞–љ–љ—Л–Љ¬†–њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ —Г–њ–Њ—А—П–і–Њ—З–µ–љ–љ–Њ–є —В—А–Њ–є–Ї–Є –≤–µ–Ї—В–Њ—А–Њ–≤ $a_1, a_2, a_3$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —З–Є—Б–ї–Њ $[a_1, a_2]a_3.$
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П:
1) –Х—Б–ї–Є $V -$ –Њ–±—К–µ–Љ –њ–∞—А–∞–ї–ї–Є–ї–µ–њ–Є–њ–µ–і–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е $a_1, a_2$ –Є $a_3,$ —В–Њ
$[a_1, a_2]a_3=V,$ –µ—Б–ї–Є —В—А–Њ–є–Ї–∞ –≤–µ–Ї—В–Њ—А–Њ–≤ $(a_1, a_2, a_3)$ –њ—А–∞–≤–∞—П;
$[a_1, a_2]a_3=-V,$ –µ—Б–ї–Є —В—А–Њ–є–Ї–∞ –≤–µ–Ї—В–Њ—А–Њ–≤ $(a_1, a_2, a_3)$ –ї–µ–≤–∞—П.
2) –Ф–ї—П —В–Њ–≥–Њ —З—В–Њ–±—Л —В—А–Є –≤–µ–Ї—В–Њ—А–∞ $a_1, a_2, a_3$ –±—Л–ї–Є –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Є –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –≤—Л–њ–Њ–ї–љ–µ–љ–Є—П —Г—Б–ї–Њ–≤–Є—П $[a_1, a_2]a_3=0.$
–Ю—Б–љ–Њ–≤–љ–Њ–µ –∞–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П —Б–Њ—Б—В–Њ–Є—В –≤ —В–Њ–Љ, —З—В–Њ —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–∞—П –њ–µ—А–µ—Б—В–∞–љ–Њ–≤–Ї–∞ –≤–µ–Ї—В–Њ—А–Њ–≤ –љ–µ –Љ–µ–љ—П–µ—В –µ–≥–Њ –≤–µ–ї–Є—З–Є–љ—Л, —В–Њ –µ—Б—В—М $[a_1, a_2]a_3=a_1[a_2, a_3]=[a_3, a_1]a_2.$
–≠—В–Њ —Б–≤–Њ–є—Б—В–≤–Њ –њ–Њ–Ј–≤–Њ–ї—П–µ—В –≤–≤–µ—Б—В–Є –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ $[a_1, a_2]a_3=a_1a_2a_3.$
–°–Љ–µ—И–∞–љ–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ —З–µ—А–µ–Ј –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–Њ–≤ –≤ –њ—А–∞–≤–Њ–Љ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ –Ј–∞–њ–Є—Б—Л–≤–∞–µ—В—Б—П –≤ –≤–Є–і–µ ¬†$$a_1a_2a_3=\begin{vmatrix}X_1&Y_1&Z_1\\X_2&Y_2&Z_2\\X_3&Y_3&Z_3\end{vmatrix}.$$
–Я—А–Є–Љ–µ—А—Л.
2.124. –Т–µ–Ї—В–Њ—А—Л $a_1, a_2, a_3$ –Њ–±—А–∞–Ј—Г—О—В –њ—А–∞–≤—Г—О —В—А–Њ–є–Ї—Г, –≤–Ј–∞–Є–Љ–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є $|a_1|=4, |a_2|=2, |a_3|=3.$ –Т—Л—З–Є—Б–ї–Є—В—М $a_1a_2a_3.$
–†–µ—И–µ–љ–Є–µ.
$a_1a_2a_3=[a_1, a_2]a_3=|[a_1, a_2]||a_3|cos(\widehat{[a_1, a_2], a_3}).$
$\cos(\widehat{[a_1, a_2], a_3})=\cos 0 =1;$
$|[a_1, a_2]|=|a_1||a_2|\sin(\widehat{a_1, a_2})=|a_1||a_2|;$
C–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, $a_1a_2a_3=|a_1||a_2||a_3|=24.$
–Ю—В–≤–µ—В: 24.
 
2.127. –£—Б—В–∞–љ–Њ–≤–Є—В—М, –Њ–±—А–∞–Ј—Г—О—В –ї–Є –≤–µ–Ї—В–Њ—А—Л $a_1, a_2$ –Є $a_3$ –±–∞–Ј–Є—Б –≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –≤—Б–µ—Е –≤–µ–Ї—В–Њ—А–Њ–≤, –µ—Б–ї–Є
–∞) $a_1(2, 3, -1), a_2(1, -1, 3), a_3(1, 9, -11);$
–±) $a_1(3, -2, 1), a_2(2, 1, 2), a_3(3, -1, -2).$
–†–µ—И–µ–љ–Є–µ.
–С–∞–Ј–Є—Б–Њ–Љ —П–≤–ї—П–µ—В—Б—П –≤—Б—П–Ї–∞—П —Г–њ–Њ—А—П–і–Њ—З–µ–љ–љ–∞—П —В—А–Њ–є–Ї–∞ –љ–µ–Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤. –Я—А–Њ–≤–µ—А–Є–Љ –±—Г–і—Г—В –ї–Є –љ–∞—И–Є –≤–µ–Ї—В–Њ—А–∞ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л, —В.–µ. –≤—Л–њ–Њ–ї–љ—П–µ—В—Б—П –ї–Є —Г—Б–ї–Њ–≤–Є–µ $a_1a_2a_3=0.$
–∞) $a_1a_2a_3=\begin{vmatrix}2&3&-1\\1&-1&3\\1&9&-11\end{vmatrix}=2\begin{vmatrix}-1&3\\9&-11\end{vmatrix}-3\begin{vmatrix}1&3\\1&-11\end{vmatrix}-\begin{vmatrix}1&-1\\1&9\end{vmatrix}=$
$=-32+42-10=0.$
–Т–µ–Ї—В–Њ—А–∞ —П–≤–ї—П—О—В—Б—П –Ї–Њ–Љ–њ–∞–ї–љ–∞—А–љ—Л–Љ–Є, —В. –µ. –Њ–љ–Є –љ–µ –Њ–±—А–∞–Ј—Г—О—В –±–∞–Ј–Є—Б.
б) $a_1a_2a_3=\begin{vmatrix}3&-2&1\\2&1&2\\3&-1&-2\end{vmatrix}=3\begin{vmatrix}1&2\\-1&-2\end{vmatrix}+2\begin{vmatrix}2&2\\3&-2\end{vmatrix}+\begin{vmatrix}2&1\\3&-1\end{vmatrix}=$ $=0-20-5=-25.$
–Т–µ–Ї—В–Њ—А–∞ –љ–µ —П–≤–ї—П—О—В—Б—П –Ї–Њ–Љ–њ–∞–ї–љ–∞—А–љ—Л–Љ–Є, —В. –µ. –Њ–љ–Є –Њ–±—А–∞–Ј—Г—О—В –±–∞–Ј–Є—Б.
–Ю—В–≤–µ—В. –∞) –љ–µ –Њ–±—А–∞–Ј—Г—О—В; –±) –Њ–±—А–∞–Ј—Г—О—В.
 
2.129. –Ф–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –њ—А–Є –ї—О–±—Л—Е $a, b$ –Є $c$ –≤–µ–Ї—В–Њ—А—Л $a-b, b-c$ –Є $c-a$ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л. –Ъ–∞–Ї–Њ–≤ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї —Н—В–Њ–≥–Њ —Д–∞–Ї—В–∞?¬†
–†–µ—И–µ–љ–Є–µ.
–Я—Г—Б—В—М $a=(x_a, y_a, z_a), b=(x_b, y_b, z_b), c=(x_c, y_c, z_c).$
–Ґ–Њ–≥–і–∞, $[a-b, b-c](c-a)=\begin{vmatrix}x_a-x_b&y_a-y_b&z_a-z_b\\x_b-x_c&y_b-y_c&z_b-z_c\\x_c-x_a&y_c-y_a&z_c-z_a\end{vmatrix}=$
–њ–Њ–ї—М–Ј—Г—П—Б—М —Б–≤–Њ–є—Б—В–≤–Њ–Љ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–є –і–Њ–±–∞–≤–Є–Љ –Ї–Њ –≤—В–Њ—А–Њ–є —Б—В—А–Њ–Ї–µ –њ–µ—А–≤—Г—О, –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М –њ—А–Є —Н—В–Њ–Љ –љ–µ –Љ–µ–љ—П–µ—В—Б—П:
$=\begin{vmatrix}x_a-x_b&y_a-y_b&z_a-z_b\\x_a-x_c&y_a-y_c&z_a-z_c\\x_c-x_a&y_c-y_a&z_c-z_a\end{vmatrix}=0$ (–Ю–њ—П—В—М –≤–Њ—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї–Є—Б—М —Б–≤–Њ–є—Б—В–≤–Њ–Љ –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї–µ–є -- –≤—В–Њ—А–∞—П –Є —В—А–µ—В—М—П —Б—В—А–Њ–Ї–Є –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л, –њ–Њ—Н—В–Њ–Љ—Г –Њ–њ—А–µ–і–µ–ї–Є—В–µ–ї—М —А–∞–≤–µ–љ –љ—Г–ї—О.)
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,¬†–≤–µ–Ї—В–Њ—А—Л $a-b, b-c$ –Є $c-a$ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л. –У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –≤ —В–Њ–Љ, —З—В–Њ –≤–µ–Ї—В–Њ—А—Л¬†$a-b, b-c$ –Є $c-a$ –ї–µ–ґ–∞—В –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ–ї–Њ—Б–Ї–Њ—Б—В—П—Е.
 
2.134. –Т —В–µ—В—А–∞—Н–і—А–µ —Б –≤–µ—А—И–Є–љ–∞–Љ–Є –≤ —В–Њ—З–Ї–∞—Е $A(1, 1, 1), B(2, 0, 2), C(2, 2, 2)$ –Є $D(3, 4, -3)$ –≤—Л—З–Є—Б–ї–Є—В—М –≤—Л—Б–Њ—В—Г $h=|\overline{DE}|.$
–†–µ—И–µ–љ–Є–µ.
–Т—Л—З–Є—Б–ї–Є–Љ –Њ–±—К–µ–Љ —В–µ—В—А–∞—Н–і—А–∞ –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $V=\frac{1}{6}|\overline{AB}\overline{AC}\overline{AD}|:$
$\overline{AB}=(1, -1, 1);$
$\overline{AC}=(1, 1, 1);$
$\overline{AD}=(2, 3, -4);$
$\overline{AB}\overline{AC}\overline{AD}=\begin{vmatrix}1&-1&1\\1&1&1\\2&3&-4\end{vmatrix}=\begin{vmatrix}1&1\\3&-4\end{vmatrix}+\begin{vmatrix}1&1\\2&-4\end{vmatrix}+\begin{vmatrix}1&1\\2&3\end{vmatrix}=$
$=-7-6+1=-12.$
 $V=\frac{1}{6}|\overline{AB}\overline{AC}\overline{AD}|=2.$
 
–Ю–±—К–µ–Љ —В–∞–Ї–ґ–µ –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ –Є–Ј–≤–µ—Б—В–љ–Њ–є —Б —И–Ї–Њ–ї—М–љ–Њ–≥–Њ –Ї—Г—А—Б–∞ —Д–Њ—А–Љ—Г–ї–µ¬†
$V=\frac{1}{3}S_{OCH}h=\frac{1}{3}S_{\triangle ABC}|DE|=\frac{1}{6}|[\overline{AB}, \overline{AC}]||DE|.$
$[\overline{AB}, \overline{AC}]=\begin{vmatrix}i&j&k\\1&-1&1\\1&1&1\end{vmatrix}=i\begin{vmatrix}-1&1\\1&1\end{vmatrix}-j\begin{vmatrix}1&1\\1&1\end{vmatrix}+k\begin{vmatrix}1&-1\\1&1\end{vmatrix}=-2i+2k.$
$|[\overline{AB}, \overline{AC}]|=\sqrt{2^2+2^2}=\sqrt{8}.$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, $2=\frac{1}{6}\sqrt{8}|DE|.$ –Ю—В—Б—О–і–∞ $|DE|=\frac{12}{\sqrt{8}}=3\sqrt 2.$
–Ю—В–≤–µ—В: $3\sqrt {2}.$
 
2.137. –Ф–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ —З–µ—В—Л—А–µ —В–Њ—З–Ї–Є $A(1, 2, -1), B(0, 1, 5), C(-1, 2, 1)$ –Є $D(2, 1,3)$ –ї–µ–ґ–∞—В –≤ –Њ–і–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є.
–†–µ—И–µ–љ–Є–µ.
–І–µ—В—Л—А–µ —В–Њ—З–Ї–Є $A, B, C$ –Є $D$ –љ–∞—Е–Њ–і—П—В—Б—П –≤ –Њ–і–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –µ—Б–ї–Є –≤–µ–Ї—В–Њ—А–∞ $\overline{AB}, \overline{AC}$ –Є $\overline{AD}$ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л.
–Я—А–Њ–≤–µ—А–Є–Љ, –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л –ї–Є —Н—В–Є –≤–µ–Ї—В–Њ—А–∞:
$\overline{AB}=(-1, -1, 6);$
$\overline{AC}=(-2, 0, 2);$
$\overline{AD}=(1, -1, 4).$
$\overline{AB}\overline{AC}\overline{AD}=\begin{vmatrix}-1&-1&6\\-2&0&2\\1&-1&4\end{vmatrix}=-\begin{vmatrix}0&2\\-1&4\end{vmatrix}+\begin{vmatrix}-2&2\\1&4\end{vmatrix}+6\begin{vmatrix}-2&0\\1&-1\end{vmatrix}=$ $=-2-10+12=0.$
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –≤–µ–Ї—В–Њ—А–∞¬†$\overline{AB}, \overline{AC}$ –Є $\overline{AD}$ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л –Є —В–Њ—З–Ї–Є¬†$A, B, C$ –Є $D$ –љ–∞—Е–Њ–і—П—В—Б—П –≤ –Њ–і–љ–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є.
 
–Ф–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ.
2.102. $|a|=|b|=5,$ $(\widehat{a, b})=\pi/4$ –Т—Л—З–Є—Б–ї–Є—В—М –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–∞–Ї–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е $a-2b,$ $3a+2b.$
–Ю—В–≤–µ—В: $50\sqrt{2}.$
 
2.104. –Ф–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ –њ—А–Є –ї—О–±—Л—Е –≤–µ–Ї—В–Њ—А–∞—Е $a, p, q$ –Є $r$ –≤–µ–Ї—В–Њ—А—Л $[a, p], [a, q]$ –Є $[a, r]$ –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л.
 
2.106. –Ч–∞–і–∞–љ—Л –≤–µ–Ї—В–Њ—А—Л $a_1(3, -1, 2)$ –Є $a_2(1, 2, -1)$. –Э–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–Њ–≤
–∞) $[a_1, a_2];$
–±) $[2a_1+a_2, a_2];$
–≤) $[2a_1-a_2, 2a_1+a_2].$
–Ю—В–≤–µ—В: –∞) $(-3, 5, 7); $ –±) $(-6, 10, 14);$ –≤) $(-12, 20, 28).$
 
2.108. –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ —Б ¬†–≤–µ—А—И–Є–љ–∞–Љ–Є¬†$A(1, -1, 2), B(5, -6, 2)$¬†–Є $C(1, 3, -1)$ –љ–∞–є—В–Є –≤—Л—Б–Њ—В—Г $h=|BD|.$
–Ю—В–≤–µ—В: 5.
 
2.111.¬†–Ф–ї—П –Ј–∞–і–∞–љ–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $a(2, 1, -1), b(1, 2, 1), c(2, -1, 3), d(3, -1, 2)$ –≤—Л—З–Є—Б–ї–Є—В—М –њ—А–Њ–µ–Ї—Ж–Є—О –≤–µ–Ї—В–Њ—А–∞ $a+c$ –љ–∞ –≤–µ–Ї—В–Њ—А $[b-d,c].$
–Ю—В–≤–µ—В: $\sqrt{6}.$
 
2.119. –Э–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $x,$ –µ—Б–ї–Є –Њ–љ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ –≤–µ–Ї—В–Њ—А–∞–Љ $a_1(2, -3, 1)$ –Є $a_2(1, -2, 3),$ –∞ —В–∞–Ї–ґ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В —Г—Б–ї–Њ–≤–Є—О $x(i+2j-7k)=10.$¬†
–Ю—В–≤–µ—В: $(7, 5, 1).$
 
2.125. –Т–µ–Ї—В–Њ—А—Л $a, b, c$ –Њ–±—А–∞–Ј—Г—О—В –ї–µ–≤—Г—О —В—А–Њ–є–Ї—Г $|a|=1, |b|=2, |c|=3,$ $(\widehat{a, b})=\pi/6, c\bot a, c\bot b.$ –Э–∞–є—В–Є $abc.$
–Ю—В–≤–µ—В: $-3/2.$
 
2.130. –Ф–Њ–Ї–∞–Ј–∞—В—М —В–Њ–ґ–і–µ—Б—В–≤–Њ $(a+b+c)(a-2b+2c)(4a+b+5c)=0.$
 
2.132. –Т—Л—З–Є—Б–ї–Є—В—М –Њ–±—К–µ–Љ —В–µ—В—А–∞—Н–і—А–∞ $OABC,$ –µ—Б–ї–Є $\overline{OA}=3i+4j, ¬†\overline{OB}=-3j+k, \overline{OC}=2j+5k.$
–Ю—В–≤–µ—В: $17/2.$
 
2.133. –Т—Л—З–Є—Б–ї–Є—В—М –Њ–±—К–µ–Љ —В–µ—В—А–∞—Н–і—А–∞ —Б –≤–µ—А—И–Є–љ–∞–Љ–Є –≤ —В–Њ—З–Ї–∞—Е $A(2, -3, 5), B(0, 2, 1), C(-2, -2, 3)$ –Є $D(3, 2, 4).$
–Ю—В–≤–µ—В: $6.$
 
2.136. –Я—А–Є –Ї–∞–Ї–Њ–Љ $\lambda$ –≤–µ–Ї—В–Њ—А—Л $a, b, c$ –±—Г–і—Г—В –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л?
–∞) $a(\lambda, 3, 1), b(5, -1, 2), c(-1, 5, 4);$
–±) $a(1, 2\lambda, 1), b(1,\lambda,0), c(0, \lambda, 1).$
–Ю—В–≤–µ—В: –∞) $-3$¬†–±) –њ—А–Є –ї—О–±–Њ–Љ¬†$\lambda.$¬†
 
2.140. –Ф–Њ–Ї–∞–Ј–∞—В—М —В–Њ–ґ–і–µ—Б—В–≤–∞
–∞) $(a+c)b(a+b)=-abc;$
–±) $(a-b)(a-b-c)(a+2b-c)=3abc;$
–≤) $(a+b)(b+c)(c+a)=2abc;$
–≥) $\forall\alpha, \beta(ab(c+\alpha a+\beta b))=abc.$


