–°–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤, —Б–≤–Њ–є—Б—В–≤–∞. –Ф–ї–Є–љ–∞ –≤–µ–Ї—В–Њ—А–Њ–≤. –£–≥–Њ–ї –Љ–µ–ґ–і—Г –≤–µ–Ї—В–Њ—А–∞–Љ–Є.
–Ы–Є—В–µ—А–∞—В—Г—А–∞: –°–±–Њ—А–љ–Є–Ї –Ј–∞–і–∞—З –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –І–∞—Б—В—М 1. –Я–Њ–і —А–µ–і –Р. –Т. –Х—Д–Є–Љ–Њ–≤–∞, –С. –Я. –Ф–µ–Љ–Є–і–Њ–≤–Є—З–∞.
 
–Ф–ї–Є–љ–∞ –≤–µ–Ї—В–Њ—А–∞.
–Я—Г—Б—В—М –≤–µ–Ї—В–Њ—А $\overline a=(x, y, z)$ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ —Б–≤–Њ–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ. –Ґ–Њ–≥–і–∞ –µ–≥–Њ –і–ї–Є–љ—Г –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$|\overline a|=\sqrt{x^2+y^2+z^2}.$$
 
–°–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤.
 
–Х—Б–ї–Є –Ј–∞–і–∞–љ—Л –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–µ–Ї $A(x_1, y_1, z_1) $ –Є $B(x_2, y_2, z_2),$ —В–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $\overline{AB}$ –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –њ–Њ —Д–Њ—А–Љ—Г–ї–∞–Љ $$\overline{AB}=(x_2-x_1, y_2-y_1, z_2-z_1).$$ –°–Ї–∞–ї—П—А–љ—Л–Љ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ–Љ –љ–µ–љ—Г–ї–µ–≤—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $a_1$ –Є $a_2$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —З–Є—Б–ї–Њ $$(a_1, a_2)=|a_1||a_2|\cos(\widehat{a_1, a_2}).$$
 
–Ф–ї—П —Б–Ї–∞–ї—П—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П –љ–∞—А—П–і—Г —Б –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ–Љ $(a_1,a_2)$ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П —В–∞–Ї–ґ–µ –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є–µ $a_1a_2.$¬†
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–Ї–∞–ї—П—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П:
1) $a_1\perp a_2\Leftrightarrow a_1a_2=0$ (—Г—Б–ї–Њ–≤–Є–µ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ—Б—В–Є –≤–µ–Ї—В–Њ—А–Њ–≤).
2) –Х—Б–ї–Є $\varphi=(\widehat{a_1, a_2}),$ —В–Њ $$0\leq\varphi<\frac{\pi}{2}\Leftrightarrow a_1a_2>0; \qquad\qquad \frac{\pi}{2}<\varphi\leq\pi\Leftrightarrow a_1 a_2<0.$$
–Р–ї–≥–µ–±—А–∞–Є—З–µ—Б–Ї–Є–µ —Б–≤–Њ–є—Б—В–≤–∞ —Б–Ї–∞–ї—П—А–љ–Њ–≥–Њ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є—П:
1) $a_1a_2=a_2a_1;$
2) $(\lambda a_1)a_2=\lambda (a_1 a_2);$
3) $a(b_1+b_2)=ab_1+ab_2.$
–Х—Б–ї–Є –≤–µ–Ї—В–Њ—А—Л $a_1(X_1, Y_1, Z_1)$ –Є $a_2(X_2, Y_2, Z_2)$ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л —Б–≤–Њ–Є–Љ–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–Љ –±–∞–Ј–Є—Б–µ, —В–Њ —Б–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ —А–∞–≤–љ–Њ $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$
–Ш–Ј —Н—В–Њ–є —Д–Њ—А–Љ—Г–ї—Л, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, —Б–ї–µ–і—Г–µ—В —Д–Њ—А–Љ—Г–ї–∞ –і–ї—П –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П –Ї–Њ—Б–Є–љ—Г—Б–∞ —Г–≥–ї–∞ –Љ–µ–ґ–і—Г –≤–µ–Ї—В–Њ—А–∞–Љ–Є:
$$\cos(\widehat{a_1, a_2})=\frac{a_1 a_2}{|a_1||a_2|}=\frac{X_1X_2+Y_1Y_2+Z_1Z_2}{\sqrt{X_1^2+Y_1^2+Z_1^2}\sqrt{X_2^2+Y_2^2+Z_2^2}}.$$
–Я—А–Є–Љ–µ—А—Л.
2.65. $|a_1|=3; |a_2|=4; (\widehat{a_1,a_2})=\frac{2\pi}{3}.$ –Т—Л—З–Є—Б–ї–Є—В—М:
–∞) $a_1^2=a_1a_1;$
–±) $(3a_1-2a_2)(a_1+2a_2);$
–≤) $(a_1+a_2)^2.$
–†–µ—И–µ–љ–Є–µ.¬†
а) $$a_1^2=(a_1, a_1)=|a_1||a_1|\cos(\widehat{a_1, a_1})=|a_1|^2=3^2=9.$$
б) $(3a_1-2a_2)(a_1+2a_2);$
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г —Б–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –Ј–∞–≤–Є—Б–Є—В –Њ—В –і–ї–Є–љ –≤–µ–Ї—В–Њ—А–Њ–≤ –Є —Г–≥–ї–∞ –Љ–µ–ґ–і—Г –љ–Є–Љ–Є, —В–Њ –Ј–∞–і–∞–љ–љ—Л–µ –≤–µ–Ї—В–Њ—А—Л –Љ–Њ–ґ–љ–Њ –≤—Л–±—А–∞—В—М –њ—А–Њ–Є–Ј–≤–Њ–ї—М–љ–Њ —Г—З–Є—В—Л–≤–∞—П —Н—В–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є. –Я—Г—Б—В—М $a_1=(3; 0). $ –Ґ–Њ–≥–і–∞ –≤–µ–Ї—В–Њ—А $a_2,$ –Є–Љ–µ—П –і–ї–Є–љ—Г $|a_2|=4,$ –Є, –Њ–±—А–∞–Ј—Г—П —Г–≥–Њ–ї $\frac{2\pi}{3}$ —Б –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ–є –њ–Њ–ї—Г–Њ—Б—М—О –Њ—Б–Є $OX,$ –Є–Љ–µ–µ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л $x=|a_2|cos\frac{2\pi}{3}=-\frac{4}{2}=-2; $¬†
$y=|a_2|\sin\frac{2\pi}{3}=4\frac{\sqrt 3}{2}=2\sqrt 3$
 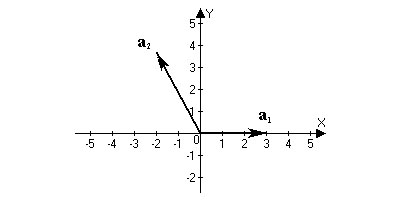
$3a_1-2a_2=3(3;0)-2(-2;2\sqrt 3)=(9;0)-(-4; 4\sqrt 3)=(13;-4\sqrt 3);$
$a_1+2a_2=(3; 0)+2(-2;2\sqrt 3) = (3; 0)+ (-4; 4\sqrt 3)= (-1; 4\sqrt 3).$
 $(3a_1-2a_2)(a_1+2a_2)=(13; -4\sqrt 3)(-1; 4\sqrt 3) =-13-48=-61.$
в) $(a_1+a_2)^2.$
$a_1+a_2$=$(3; 0)+(-2; 2\sqrt 3)=(1; 2\sqrt 3).$
$(a_1+a_2)^2=(1; 2\sqrt3) (1; 2\sqrt 3)=1+12=13.$
–Ю—В–≤–µ—В: a) 9; ¬†–±) -61; –≤) 13.
 {jumi[*4]}
2.67. –Т—Л—З–Є—Б–ї–Є—В—М –і–ї–Є–љ—Г –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞, –њ–Њ—Б—В—А–Њ–µ–љ–љ–Њ–≥–Њ –љ–∞ –≤–µ–Ї—В–Њ—А–∞—Е $a=p-3q, $ $b=5p+2q,$¬†–µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ $|p|=2\sqrt{2}, |q|=3, (\widehat{p, q})=\frac{\pi}{4}.$¬†
–†–µ—И–µ–љ–Є–µ.¬†
 –°–њ–Њ—Б–Њ–± 1.
–°–њ–Њ—Б–Њ–± 1.
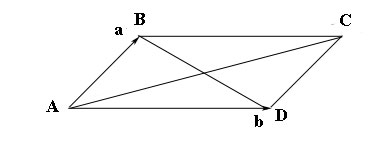
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABC$ –Є–Љ–µ–µ–Љ $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$¬†
–Ч–љ–∞—П –і–ї–Є–љ—Г –≤–µ–Ї—В–Њ—А–Њ–≤ $p$ b $q$¬†–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г —Н—В–Є–Љ–Є –≤–µ–Ї—В–Њ—А–∞–Љ–Є, –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –і–ї–Є–љ—Г –≤–µ–Ї—В–Њ—А–∞ $AC$¬†–њ–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤:
$|AC|^2=|6p|^2+|q|^2-12pq\cos\widehat{(6p, q)}=288+9-72=225.$
–Ю—В—Б—О–і–∞ $|AC|=15.$
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABD$ –Є–Љ–µ–µ–Љ:¬†$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$
–Я–Њ —В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤ –љ–∞—Е–Њ–і–Є–Љ –і–ї–Є–љ—Г –≤–µ–Ї—В–Њ—А–∞ $BD:$
$|BD|^2=|4p|^2+|5q|^2-8p5q\cos \widehat{(6p, q)}=$ $128+225+240=593.$
–Ю—В—Б—О–і–∞ $|BD|=\sqrt{593}.$
 
¬†–°–њ–Њ—Б–Њ–± 2.
–Я—Г—Б—В—М $q=(3; 0). $ –Ґ–Њ–≥–і–∞ –≤–µ–Ї—В–Њ—А $p,$ –Є–Љ–µ—П –і–ї–Є–љ—Г $|p|=2\sqrt 2,$ –Є –Њ–±—А–∞–Ј—Г—П —Г–≥–Њ–ї $\frac{\pi}{4}$ —Б –њ–Њ–ї–Њ–ґ–Є—В–µ–ї—М–љ–Њ–є –њ–Њ–ї—Г–Њ—Б—М—О –Њ—Б–Є $OX$ –Є–Љ–µ–µ—В –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л
$x=|p|\cos\frac{\pi}{4}=2\sqrt 2\frac{1}{\sqrt 2}=2; $
$y=|p|\sin\frac{\pi}{4}=2\sqrt 2\frac{1}{\sqrt 2}=2.$ 
 
–Т–µ–Ї—В–Њ—А $BC=AD=b.$
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABC$ –Є–Љ–µ–µ–Љ
$AC=AB+BC=a+b=p-3q+5p+2q=6p-q=$ $=6(2;2)-(3;0)=(12; 12)-(3;0)=(9; 12).$
¬†–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, $|AC|=\sqrt{81+144}=\sqrt{225}=15.$
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABD$ –Є–Љ–µ–µ–Љ¬†
$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$ 
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, $|BD|=\sqrt{23^2+8^2}=\sqrt {593}.$
–Ю—В–≤–µ—В:¬†$15, \sqrt {593}.$
 
2.68. –Ю–њ—А–µ–і–µ–ї–Є—В—М —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –≤–µ–Ї—В–Њ—А–∞–Љ–Є $a$ –Є $b$ –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ $(a-b)^2+(a+2b)^2=20$ –Є $|a|=1, |b|=2.$
–Ю—В–≤–µ—В: $2\pi/3$
–Ф–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ:
2.66.
$|a_1|=3; |a_2|=5. $ –Ю–њ—А–µ–і–µ–ї–Є—В—М, –њ—А–Є –Ї–∞–Ї–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–Є $\alpha$ –≤–µ–Ї—В–Њ—А—Л $a_1+\alpha a_2$ –Є $a_1-\alpha a_2$¬†–±—Г–і—Г—В –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л.
–Ю—В–≤–µ—В: $\alpha=\pm\frac{3}{5}$
 
2.69. 
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ $ABC$ $\overline{AB}=3e_1-4e_2;$ $\overline{BC}=e_1+5e_2.$ –Т—Л—З–Є—Б–ї–Є—В—М –і–ї–Є–љ—Г –µ–≥–Њ –≤—Л—Б–Њ—В—Л $\overline{CH},$¬†–µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ $e_1$ –Є $e_2$ –≤–Ј–∞–Є–Љ–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л–µ –Њ—А—В—Л.
–Ю—В–≤–µ—В: $\frac{19}{5}.$
 


