–С–∞–Ј–Є—Б –ї–Є–љ–µ–є–љ–Њ–≥–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞. –†–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ –њ–Њ –±–∞–Ј–Є—Б—Г.
 
–Ы–Є—В–µ—А–∞—В—Г—А–∞: –°–±–Њ—А–љ–Є–Ї –Ј–∞–і–∞—З –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –І–∞—Б—В—М 1. –Я–Њ–і —А–µ–і –Р. –Т. –Х—Д–Є–Љ–Њ–≤–∞, –С. –Я. –Ф–µ–Љ–Є–і–Њ–≤–Є—З–∞.
–£–њ–Њ—А—П–і–Њ—З–µ–љ–љ–∞—П —В—А–Њ–є–Ї–∞ –љ–µ–Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $e_1, e_2, e_3$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –±–∞–Ј–Є—Б–Њ–Љ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –≤—Б–µ—Е –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –≤–µ–Ї—В–Њ—А–Њ–≤. –Т—Б—П–Ї–Є–є –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є –≤–µ–Ї—В–Њ—А $a$ –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Л–Љ –Њ–±—А–∞–Ј–Њ–Љ –≤ –≤–Є–і–µ $$a=X_1e_1+X_2e_2+X_3e_3.\qquad\qquad\qquad\qquad\qquad (1)$$ –І–Є—Б–ї–∞ $X_1, X_2, X_3$ –љ–∞–Ј—Л–≤–∞—О—В—Б—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞–Љ–Є –≤–µ–Ї—В–Њ—А–∞ –≤ –±–∞–Ј–Є—Б–µ $B=\{e_1, e_2, e_3\}.$ –Ч–∞–њ–Є—Б—М (1) –љ–∞–Ј—Л–≤–∞—О—В —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ–Љ –≤–µ–Ї—В–Њ—А–∞ $a$ –њ–Њ –±–∞–Ј–Є—Б—Г $B.$
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ, —Г–њ–Њ—А—П–і–Њ—З–µ–љ–љ–∞—П –њ–∞—А–∞ –љ–µ–Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л—Е –≤–µ–Ї—В–Њ—А–Њ–≤ $e_1, e_2$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –±–∞–Ј–Є—Б–Њ–Љ $B=(e_1, e_2)$ –≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –≤–µ–Ї—В–Њ—А–Њ–≤, –Ї–Њ–Љ–њ–ї–∞–љ–∞—А–љ—Л—Е –љ–µ–Ї–Њ—В–Њ—А–Њ–є –њ–ї–Њ—Б–Ї–Њ—Б—В–Є.¬†
–Э–∞–Ї–Њ–љ–µ—Ж, –≤—Б—П–Ї–Є–є –љ–µ–љ—Г–ї–µ–≤–Њ–є –≤–µ–Ї—В–Њ—А $e$ –Њ–±—А–∞–Ј—Г–µ—В –±–∞–Ј–Є—Б $B=(e)$ –≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є—Е –≤–µ–Ї—В–Њ—А–Њ–≤, –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л—Е –љ–µ–Ї–Њ—В–Њ—А–Њ–Љ—Г –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—О.¬†
–Х—Б–ї–Є –≤–µ–Ї—В–Њ—А $a$ –µ—Б—В—М –ї–Є–љ–µ–є–љ–∞—П –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –≤–µ–Ї—В–Њ—А–Њ–≤ $a_1, a_2, ..., a_n$ —Б –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞–Љ–Є $\lambda_1, \lambda_2, ...,\lambda_n$, —В–Њ –µ—Б—В—М $$a=\sum\limits_{k=1}^n \lambda_ka_k$$ —В–Њ –Ї–∞–ґ–і–∞—П –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ $X_i(a)$ –≤–µ–Ї—В–Њ—А–∞ $a$ —А–∞–≤–љ–∞ —Б—Г–Љ–Љ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ $\lambda_1,\lambda_2,..., \lambda_n$ –љ–∞ –Њ–і–љ–Њ–Є–Љ–µ–љ–љ—Л–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–Њ–≤ $a_1, a_2, ..., a_n: $ $$X_i(a)=\sum\limits_{k=1}^n\lambda_k X_i(a_k),\qquad (i=1, 2, 3.)$$
–С–∞–Ј–Є—Б $B=(e_1, e_2, e_3)$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–Љ, –µ—Б–ї–Є –≤–µ–Ї—В–Њ—А—Л $e_1, e_2$ –Є $e_3$ –њ–Њ–њ—А–∞–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є –Є–Љ–µ—О—В –µ–і–Є–љ–Є—З–љ—Г—О –і–ї–Є–љ—Г. –Т —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ –њ—А–Є–љ—П—В—Л –Њ–±–Њ–Ј–љ–∞—З–µ–љ–Є—П ¬†$$e_1=i;\,\, e_2-j;\,\, e_3=k.$$
–Я—А–Є–Љ–µ—А—Л.
2.26. –Ч–∞–і–∞–љ —В–µ—В—А–∞—Н–і—А $OABC.$ –Т –±–∞–Ј–Є—Б–µ –Є–Ј —А–µ–±–µ—А $\overline{OA}, \overline{OB}$ –Є¬†$\overline{OC}$¬†¬†–љ–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л:
–∞) –≤–µ–Ї—В–Њ—А–∞ $\overline{DE},$ –≥–і–µ $D$ –Є $E$ —Б–µ—А–µ–і–Є–љ—Л —А–µ–±–µ—А $OA$ –Є $BC.$
–±) –≤–µ–Ї—В–Њ—А–∞ $\overline{OF},$ –≥–і–µ $F-$ —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –Љ–µ–і–Є–∞–љ –Њ—Б–љ–Њ–≤–∞–љ–Є—П $ABC.$
–†–µ—И–µ–љ–Є–µ.
–∞)
 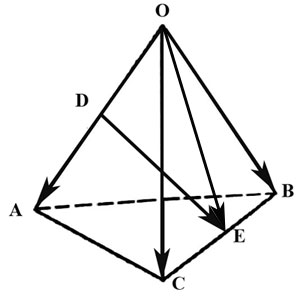
–Т—Л—А–∞–Ј–Є–Љ –≤–µ–Ї—В–Њ—А $\overline{DE}$ —З–µ—А–µ–Ј –≤–µ–Ї—В–Њ—А–∞ $\overline{OA}, \overline{OB}, \overline{OC}:$
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ODE$ –Є–Љ–µ–µ–Љ $\overline{DE}=\overline{DO}+\overline{OE}.\qquad\qquad\qquad (1)$
–Ф–∞–ї–µ–µ, $\overline{DO}=-\overline{OD}=-\frac{1}{2}\overline{OA};$
–≤–µ–Ї—В–Њ—А $\overline{OE}$ –љ–∞–є–і–µ–Љ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $OBE:$
$\overline{OE}=\overline{OB}+\overline{BE}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2),$
–Ј–і–µ—Б—М $\overline{BE}=\frac{1}{2}\overline{BC},$ –∞ –≤–µ–Ї—В–Њ—А $\overline{BC}$ –љ–∞—Е–Њ–і–Є–Љ¬†–Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $OBC:$
$\overline{BC}=\overline{BO}+\overline{OC}=\overline{OC}-\overline{OB}.$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Є–Ј (2) –њ–Њ–ї—Г—З–∞–µ–Љ¬†$\overline{OE}=\overline{OB}+\frac{1}{2}(\overline{OC}-\overline{OB}).$
–Э–∞–Ї–Њ–љ–µ—Ж –Є–Ј (1) –Є–Љ–µ–µ–Љ¬†¬†$$\overline{DE}=\overline{DO}+\overline{OE}=-\frac{1}{2}\overline{OA}+\overline{OB}+\frac{1}{2}(\overline{OC}-\overline{OB})=$$ $$=-\frac{1}{2}\overline{OA}+\frac{1}{2}\overline{OB}+\frac{1}{2}\overline{OC}.$$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $\overline{DE}$ –≤ –±–∞–Ј–Є—Б–µ –Є–Ј —А–µ–±–µ—А ¬†$\overline{OA}, \overline{OB}, \overline{OC}:$ $\left(-\frac{1}{2},\frac{1}{2},\frac{1}{2}\right).$
–Ю—В–≤–µ—В:¬†$\left(-\frac{1}{2}; \frac{1}{2}; \frac{1}{2}\right).$
б) 
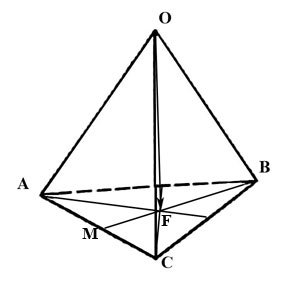
¬†–Т—Л—А–∞–Ј–Є–Љ –≤–µ–Ї—В–Њ—А $\overline{OF}$ —З–µ—А–µ–Ј –≤–µ–Ї—В–Њ—А–∞ $\overline{OA}, \overline{OB}, \overline{OC}:$
–Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $OFB$ –Є–Љ–µ–µ–Љ $\overline{OF}=\overline{OB}+\overline{BF}.\qquad\qquad\qquad (1)$
–Ф–∞–ї–µ–µ, $\overline{BF}=\frac{2}{3}\overline{BM};$
–≤–µ–Ї—В–Њ—А $\overline{BM}$ –љ–∞–є–і–µ–Љ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $BMC:$
$\overline{BM}=\overline{BC}+\overline{CM}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad (2)$
–Ј–і–µ—Б—М $\overline{CM}=\frac{1}{2}\overline{CA},$ –∞ –≤–µ–Ї—В–Њ—А $\overline{CA}$ –љ–∞—Е–Њ–і–Є–Љ¬†–Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $OCA:$
$\overline{CA}=\overline{CO}+\overline{OA}=-\overline{OC}+\overline{OA};$
$\overline{BC}=\overline{BO}+\overline{OC}=\overline{OC}-\overline{OB}.$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Є–Ј (2) –њ–Њ–ї—Г—З–∞–µ–Љ¬†$$\overline{BM}=\overline{BC}+\overline{CM}=\overline{OC}-\overline{OB}+\frac{1}{2}\overline{CA}=$$ $$=\overline{OC}-\overline{OB}+\frac{1}{2}(-\overline{OC}+\overline{OA}).$$
–Э–∞–Ї–Њ–љ–µ—Ж –Є–Ј (1) –Є–Љ–µ–µ–Љ¬†¬†$$\overline{OF}=\overline{OB}+\overline{BF}=\overline{OB}+\frac{2}{3}\overline{BM}=$$¬†$$=\overline{OB}+\frac{2}{3}\left(\overline{OC}-\overline{OB}+\frac{1}{2}(-\overline{OC}+\overline{OA})\right)=$$¬†$$=\overline{OB}+\frac{2}{3}\overline{OC}-\frac{2}{3}\overline{OB}+\frac{1}{3}(-\overline{OC}+\overline{OA})=\frac{1}{3}\overline{OA}+\frac{1}{3}\overline{OB}+\frac{1}{3}\overline{OC}.$$¬†
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $\overline{OF}$ –≤ –±–∞–Ј–Є—Б–µ –Є–Ј —А–µ–±–µ—А ¬†$\overline{OA}, \overline{OB}, \overline{OC}:$ $\left(\frac{1}{3}; \frac{1}{3}; \frac{1}{3}\right).$
–Ю—В–≤–µ—В:¬†$\left(\frac{1}{3}; \frac{1}{3}; \frac{1}{3}\right).$
  {jumi[*4]}
2.27. –Т —В–µ—В—А–∞—Н–і—А–µ $OABC$ –Љ–µ–і–Є–∞–љ–∞ $AL$ –≥—А–∞–љ–Є $ABC$ –і–µ–ї–Є—В—Б—П —В–Њ—З–Ї–Њ–є $M$ –≤ –Њ—В–љ–Њ—И–µ–љ–Є–Є $|\overline{AM}|:|\overline{ML}|=3:7.$ –Э–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $\overline{OM}$ –≤ –±–∞–Ј–Є—Б–µ –Є–Ј —А–µ–±–µ—А $\overline{OA}, \overline{OB}, \overline{OC}.$
–†–µ—И–µ–љ–Є–µ.
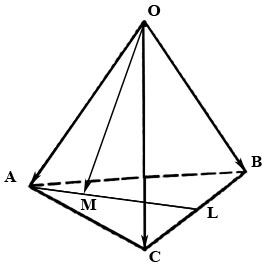
–Т–µ–Ї—В–Њ—А $\overline{OM}$ –љ–∞–є–і–µ–Љ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $AOM:$ $$\overline{OM}=\overline{OA}+\overline{AM}.\qquad\qquad\qquad (1)$$
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П¬†$|\overline{AM}|:|\overline{ML}|=3:7$ –Є–Љ–µ–µ–Љ¬†$\overline{AM}=\frac{3}{10}\overline{AL}.$ –Ш–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABL$ –љ–∞—Е–Њ–і–Є–Љ $\overline{AL}=\overline{AB}+\overline{BL}=\overline{AB}+\frac{1}{2}\overline{BC}.$
–Ф–∞–ї–µ–µ, –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ $AOB$ –Є $BOC$ –њ–Њ–ї—Г—З–∞–µ–Љ¬†
$\overline{AB}=\overline{AO}+\overline{OB}=-\overline{OA}+\overline{OB}.$
 
$\overline{BC}=\overline{BO}+\overline{OC}=\overline{OC}-\overline{OB}.$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,
$$\overline{AM}=\frac{3}{10}\overline{AL}=\frac{3}{10}\left(\overline{AB}+\frac{1}{2}\overline{BC}\right)=\frac{3}{10}\left(-\overline{OA}+\overline{OB}+\frac{1}{2}(\overline{OC}-\overline{OB})\right)=$$ $=-\frac{3}{10}\overline{OA}+\frac{3}{20}\overline{OB}+\frac{3}{20}\overline{OC}.$
–Ю—В—Б—О–і–∞ –Є –Є–Ј (1) –њ–Њ–ї—Г—З–∞–µ–Љ¬†$$\overline{OM}=\overline{OA}+\overline{AM}=\overline{OA}+\frac{3}{10}\overline{OA}+\frac{3}{20}\overline{OB}+\frac{3}{20}\overline{OC}=$$ $$=\frac{7}{10}\overline{OA}-\frac{3}{20}\overline{OB}+\frac{3}{20}\overline{OC}.$$
–Ю—В–≤–µ—В: $\left(\frac{7}{10}; \frac{3}{20};\frac{3}{20}\right).$
 
2.29. –Т —В—А–∞–њ–µ—Ж–Є–Є $ABCD$ –Є–Ј–≤–µ—Б—В–љ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –і–ї–Є–љ –Њ—Б–љ–Њ–≤–∞–љ–Є–є ¬†$|\overline{AB}|/|\overline{CD}|=\lambda$ –Э–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $\overline{CB}$ –≤ –±–∞–Ј–Є—Б–µ –Є–Ј –≤–µ–Ї—В–Њ—А–Њ–≤ $\overline{AB}$ –Є $\overline{AD}.$
–†–µ—И–µ–љ–Є–µ.
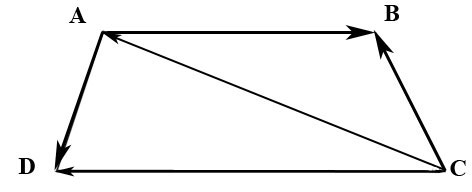
–Т–µ–Ї—В–Њ—А $\overline{CB}$ –Љ–Њ–ґ–љ–Њ –љ–∞–є—В–Є –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ABC:$ $\overline{CB}=\overline{CA}+\overline{AB}.$
$\overline{CA}$ –љ–∞—Е–Њ–і–Є–Љ –Є–Ј —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ $ACD:$ $\overline{CA}=\overline{CD}+\overline{DA}=\overline{CD}-\overline{AD}.$
–Ш–Ј —Г—Б–ї–Њ–≤–Є—П¬†¬†$|\overline{AB}|/|\overline{CD}|=\lambda$ –љ–∞—Е–Њ–і–Є–Љ –≤–µ–Ї—В–Њ—А $\overline{CD}:$ $\overline{CD}=-\overline{AB}/\lambda.$
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, $\overline{CA}=-\overline{AB}/\lambda-\overline{AD};$
$\overline{CB}=-\overline{AB}/\lambda-\overline{AD}+\overline{AB}=\left(1-\frac{1}{\lambda}\right)\overline{AB}-\overline{AD}.$
–Ю—В–≤–µ—В: $\left(1-\frac{1}{\lambda}; -1\right).$
 
2.36. –Ч–∞–і–∞–љ—Л –≤–µ–Ї—В–Њ—А—Л $e(-1, 1, 1/2)$ –Є $a(2, -2, -1).$ –£–±–µ–і–Є—В—М—Б—П, —З—В–Њ –Њ–љ–Є –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л –Є –љ–∞–є—В–Є —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ $a$ –њ–Њ –±–∞–Ј–Є—Б—Г $B(e). $¬†
–†–µ—И–µ–љ–Є–µ.¬†
–Т–µ–Ї—В–Њ—А—Л –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л, –µ—Б–ї–Є –Є—Е –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П —Б–Њ–≤–њ–∞–і–∞—О—В –Є–ї–Є –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л, —В.–µ. —В–Њ–≥–і–∞ –Є —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞ –Ї–Њ–≥–і–∞ –Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ—Л. –Я—А–Њ–≤–µ—А–Є–Љ: $$\frac{-1}{2}=\frac{1}{-2}=\frac{1/2}{-1}=-\frac{1}{2},$$ —В–Њ –µ—Б—В—М –≤–µ–Ї—В–Њ—А—Л $e$ –Є $a$ –Ї–Њ–ї–ї–Є–љ–µ–∞—А–љ—Л.
–Э–∞–є–і–µ–Љ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ $a$ –њ–Њ –±–∞–Ј–Є—Б—Г $B(e),$¬†—В–Њ –µ—Б—В—М –љ–∞–є–і–µ–Љ —В–∞–Ї–Њ–µ —З–Є—Б–ї–Њ $\lambda$ —З—В–Њ $a=\lambda e:$
 
$$\left\{\begin{array}{lcl}2=-\lambda\\ -2=\lambda\\-1=\frac{1}{2}\lambda\end{array}\right.\Rightarrow \lambda=-2,$$
–Ю—В—Б—О–і–∞ $a=-2e.$
–Ю—В–≤–µ—В: $a=-2e.$
 
 
–Ф–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ.
2.28. –Т–љ–µ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ $ABCD$ –≤–Ј—П—В–∞ —В–Њ—З–Ї–∞ $O.$ –Т –±–∞–Ј–Є—Б–µ –Є–Ј –≤–µ–Ї—В–Њ—А–Њ–≤ $\overline{OA}, \overline{OB}$ –Є $\overline{OC}$ –љ–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л:
–∞) –≤–µ–Ї—В–Њ—А–∞¬†$\overline{OM}$¬†, –≥–і–µ $M$ —В–Њ—З–Ї–∞ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –і–Є–∞–≥–Њ–љ–∞–ї–µ–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞;
–±) –≤–µ–Ї—В–Њ—А–∞ $\overline{OK},$ –≥–і–µ $K$- —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л $AD.$
¬†–Ю—В–≤–µ—В: –∞) $(1/2; 0; 1/2);$ –±) $(1, -1/2, 1/2).$¬†
2.31. –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ $ABC$ $\overline{AK}=\alpha\overline{AB}; \overline{BM}=\beta\overline{BC};$ $\overline{CF}=\gamma\overline{CA}.$ –Я—Г—Б—В—М $P, Q$ –Є $R -$ —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –њ—А—П–Љ—Л—Е $BF$ –Є $CK;$ $CK$ –Є $AM;$ $AM$ –Є $BF$ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Т –±–∞–Ј–Є—Б–µ –Є–Ј –≤–µ–Ї—В–Њ—А–Њ–≤ $\overline{AB}$ –Є $\overline{AC}$ –љ–∞–є—В–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–Њ–≤ $\overline{AP},$ $\overline{BQ}$ –Є $\overline{CR}.$
–Ю—В–≤–µ—В:¬†$\overline{AP}\left(\frac{\alpha(1-\gamma)}{1-\alpha\gamma}; \frac{\gamma(1-\alpha)}{1-\alpha\gamma}\right);$¬†$\overline{BQ}\left(\frac{2\alpha\beta-\alpha-\beta}{1-\alpha\beta}; \frac{\beta(1-\alpha)}{1-\alpha\beta}\right);$¬†$\overline{CQ}\left(\frac{\beta(1-\gamma)}{1-\beta\gamma}; \frac{2\beta\gamma-\beta-\gamma}{1-\beta\gamma}\right).$
 
2.37. –Э–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –Ј–∞–і–∞–љ—Л –≤–µ–Ї—В–Њ—А—Л $e_1(-1,2),$ $e_2(2,1)$ –Є $a(0,-2).$ –£–±–µ–і–Є—В—М—Б—П, —З—В–Њ –±–∞–Ј–Є—Б $B=e_1, e_2$ –≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –≤—Б–µ—Е –≤–µ–Ї—В–Њ—А–Њ–≤ –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є –Я–Њ—Б—В—А–Њ–Є—В—М –Ј–∞–і–∞–љ–љ—Л–µ –≤–µ—В–Ї–Њ—А—Л –Є –љ–∞–є—В–Є —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ $a$ –њ–Њ –±–∞–Ј–Є—Б—Г $B.$¬†
–Ю—В–≤–µ—В: $a=-\frac{4}{5}e_1-\frac{2}{5}e_2.$
2.38.¬†–Я–Њ–Ї–∞–Ј–∞—В—М, —З—В–Њ —В—А–Њ–є–Ї–∞ –≤–µ–Ї—В–Њ—А–Њ–≤ $e_1(1,0,0), e_2(1,1,0)$ –Є $e_3(1,1,1)$ –Њ–±—А–∞–Ј—Г—О—В –±–∞–Ј–Є—Б –≤ –Љ–љ–Њ–ґ–µ—Б—В–≤–µ –≤—Б–µ—Е –≤–µ–Ї—В–Њ—А–Њ–≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞. –Т—Л—З–Є—Б–ї–Є—В—М –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л –≤–µ–Ї—В–Њ—А–∞ $a=-2i-k$ –≤ –±–∞–Ј–Є—Б–µ $B(e_1, e_2, e_3)$ –Є –љ–∞–њ–Є—Б–∞—В—М —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–∞ –њ–Њ –±–∞–Ј–Є—Б—Г.¬†
–Ю—В–≤–µ—В:¬†$a=-2e_1+e_2-e_3.$


