–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є.
–Ы–Є—В–µ—А–∞—В—Г—А–∞: –°–±–Њ—А–љ–Є–Ї –Ј–∞–і–∞—З –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –І–∞—Б—В—М 1. –Я–Њ–і —А–µ–і –Р. –Т. –Х—Д–Є–Љ–Њ–≤–∞, –С. –Я. –Ф–µ–Љ–Є–і–Њ–≤–Є—З–∞.
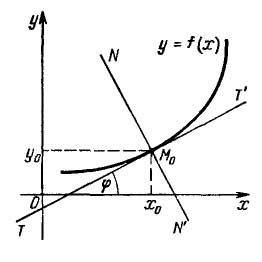
–Ч–љ–∞—З–µ–љ–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є $f'(x_0)$ —Д—Г–љ–Ї—Ж–Є–Є $y=f(x)$ –≤ —В–Њ—З–Ї–µ $x_0$ —А–∞–≤–љ–Њ —Г–≥–ї–Њ–≤–Њ–Љ—Г –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Г $k=tg\varphi$ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є $TT'$ –Ї –≥—А–∞—Д–Є–Ї—Г —Н—В–Њ–є¬†—Д—Г–љ–Ї—Ж–Є–Є, –њ—А–Њ–≤–µ–і–µ–љ–љ–Њ–є —З–µ—А–µ–Ј —В–Њ—З–Ї—Г $M_0(x_0, y_0),$ –≥–і–µ $y_0=f(x_0)$ (–≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–є —Б–Љ—Л—Б–ї –њ—А–Њ–Є–Ј–≤–Њ–і–љ–Њ–є).–Я—А—П–Љ–∞—П $NN',$ –њ—А–Њ—Е–Њ–і—П—Й–∞—П —З–µ—А–µ–Ј —В–Њ—З–Ї—Г –Ї–∞—Б–∞–љ–Є—П $M_0$ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –Ї –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є, –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –љ–Њ—А–Љ–∞–ї—М—О –Ї –≥—А–∞—Д–Є–Ї—Г —Д—Г–љ–Ї—Ж–Є–Є $y=f(x)$ –≤ —Н—В–Њ–є —В–Њ—З–Ї–µ. –£—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є $$(x-x_0)+f'(x_0)(y-y_0)=0.$$–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є $TT'$ –Ї –≥—А–∞—Д–Є–Ї—Г —Д—Г–љ–Ї—Ж–Є–Є $y=f(x)$ –≤ –µ–≥–Њ —В–Њ—З–Ї–µ $M_0(x_0, y_0)$ –Є–Љ–µ–µ—В –≤–Є–і $$y-y_0=f'(x_0)(x-x_0)$$
–£–≥–ї–Њ–Љ $\omega$ –Љ–µ–ґ–і—Г –Ї—А–Є–≤—Л–Љ–Є $y=f_1(x)$ –Є $y=f_2(x)$ –≤ –Є—Е –Њ–±—Й–µ–є —В–Њ—З–Ї–µ $M_0(x_0, y_0)$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є –Ї —Н—В–Є–Љ –Ї—А–Є–≤—Л–Љ –≤ —В–Њ—З–Ї–µ $M_0.$ –Х–≥–Њ –Љ–Њ–ґ–љ–Њ –≤—Л—З–Є—Б–ї–Є—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$tg\,\omega=\frac{f_2'(x_0)-f'_1(x_0)}{1+f'_1(x_0)f'_2(x_0)}.$$
–Я—А–Є–Љ–µ—А—Л.
–Э–∞–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Є –љ–Њ—А–Љ–∞–ї–Є –Ї –≥—А–∞—Д–Є–Ї—Г —Д—Г–љ–Ї—Ж–Є–Є $y=f(x)$ –≤ –і–∞–љ–љ–Њ–є —В–Њ—З–Ї–µ, –µ—Б–ї–Є:
5.235. $y=x^2-5x+4,$ $x_0=-1.$
–†–µ—И–µ–љ–Є–µ.
–£—А–∞–≤–љ–µ–љ–Є–µ¬†–Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ¬†$y-y_0=f'(x_0)(x-x_0);$ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є - –њ–Њ —Д–Њ—А–Љ—Г–ї–µ¬†$(x-x_0)+f'(x_0)(y-y_0)=0.$
¬†–Я–Њ —Г—Б–ї–Њ–≤–Є—О, $x_0=-1.$
$y_0=y(x_0)=(-1)^2-5\cdot(-1)+4=1+5+4=10.$
$y'(x)=2x-5\Rightarrow y'(x_0)=y'(-1)=2\cdot (-1)-5=-2-5=-7.$
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤—Б–µ –љ–∞–є–і–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:
$y-10=-7(x+1)\Rightarrow 7x+y-3=0.$
–Ґ–µ–њ–µ—А—М –љ–∞—Е–Њ–і–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:
$(x+1)-7(y-10)=0\Rightarrow x-7y+71=0.$
–Ю—В–≤–µ—В: –£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$7x+y-3=0;$¬†¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$ x-7y+71=0.$
 
5.237. $y=\sqrt x,$ $x_0=4.$
–†–µ—И–µ–љ–Є–µ.
–£—А–∞–≤–љ–µ–љ–Є–µ¬†–Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –±—Г–і–µ–Љ –Є—Б–Ї–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ¬†$y-y_0=f'(x_0)(x-x_0);$ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є - –њ–Њ —Д–Њ—А–Љ—Г–ї–µ¬†$(x-x_0)+f'(x_0)(y-y_0)=0.$
¬†–Я–Њ —Г—Б–ї–Њ–≤–Є—О, $x_0=4.$
$y_0=y(x_0)=\sqrt 4=2.$
$y'(x)=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt x}\Rightarrow y'(x_0)=y'(4)=\frac{1}{2\sqrt 4}=\frac{1}{4}.$
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤—Б–µ –љ–∞–є–і–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:
$y-2=\frac{1}{4}(x-4)\Rightarrow 4(y-2)=x-4\Rightarrow 4y-8=x-4\Rightarrow x-4y+4=0.$
–Ґ–µ–њ–µ—А—М –љ–∞—Е–Њ–і–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:
$(x-4)+\frac{1}{4}(y-2)=0\Rightarrow 4(x-4)+(y-2)=0\Rightarrow 4x+y-18=0.$
–Ю—В–≤–µ—В:¬†–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$x-4y+4=0;$¬†¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$4x+y-18=0.$
 
5.241.¬†–Э–∞–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Є –љ–Њ—А–Љ–∞–ї–Є –≤ —В–Њ—З–Ї–µ $M_0(2, 2)$ –Ї –Ї—А–Є–≤–Њ–є $x=\frac{1+t}{t^3},$ $y=\frac{3}{2t^2}+\frac{1}{2t},\,\, t\neq 0.$
–†–µ—И–µ–љ–Є–µ.
–Э–∞–є–і–µ–Љ –Ј–љ–∞—З–µ–љ–Є–µ $t_0,$ –њ–Њ–і—Б—В–∞–≤–ї—П—П –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є $M_0$ –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ї—А–Є–≤–Њ–є:¬†$2=\frac{1+t}{t^3},$ $2=\frac{3}{2t^2}+\frac{1}{2t}.$
 $\left\{\begin{array}{rcl} 2=\frac{1+t}{t^3},\\ 2=\frac{3}{2t^2}+\frac{1}{2t},\end{array}\right.\Rightarrow$ $2=\frac{1+t}{t^3}=\frac{3}{2t^2}+\frac{1}{2t}$
–†–µ—И–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ ¬†
$\frac{1+t}{t^3}=\frac{3}{2t^2}+\frac{1}{2t}$
$2(1+t)=3t+t^2\Rightarrow$
$t^2+t-2=0\Rightarrow t_1=1, t_2=-2.$
–Я–Њ–і—Б—В–∞–≤–Є–Љ –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ —А–µ—И–µ–љ–Є—П –≤ —А–∞–≤–µ–љ—Б—В–≤–Њ¬†$\frac{1+t}{t^3}=\frac{3}{2t^2}+\frac{1}{2t}:$
$t_1=1: \frac{1+1}{1}=\frac{3}{2}+\frac{1}{2}=2$
$t_2=-2: \frac{1-2}{-8}=\frac{3}{8}-\frac{1}{4}=\frac{1}{8}\neq 2$ -- –љ–µ —Г–і–Њ–≤–ї–µ—В–≤–Њ—А—П–µ—В –љ–∞—И–µ–є —Б–Є—Б—В–µ–Љ–µ.
–Э–∞–є–і–µ–Љ –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Г—О —Д—Г–љ–Ї—Ж–Є–Є, –Ј–∞–і–∞–љ–љ–Њ–є –њ–∞—А–∞–Љ–µ—В—А–Є—З–µ—Б–Ї–Є $y'_x.$
$y'_t=\left(\frac{3}{2}t^{-2}+\frac{1}{2}t^{-1}\right)'=\frac{3}{2}\cdot (-2)t^{-3}+\frac{1}{2}\cdot (-1)t^{-2}=-3t^{-3}-\frac{1}{2}t^{-2}$ 
$y'_t|_{t=1}=-3-1/2=-3,5;$
$x'_t=\left(\frac{1+t}{t^3}\right)'=\frac{(1+t)'t^3-(1+t)(t^3)'}{t^6}=\frac{t^3-(1+t)3t^2}{t^6}=\frac{t^3-3t^2-3t^3}{t^6}=\frac{-3t^2-2t^3}{t^6}.$ 
$x'_t|_{t=1}=-3-2=-5;$
$y'_x=\frac{y'_t}{x_t}.$
$y'_x|_{t=1}=\frac{-3,5}{-5}=\frac{7}{10}.$
 
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤—Б–µ –љ–∞–є–і–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П –≤ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:
$y-y_0=f'(x_0)(x-x_0)\Rightarrow$ $y-2=\frac{7}{10}(x-2)\Rightarrow 10(y-2)=7(x-2)\Rightarrow 10y-20=7x-14\Rightarrow$ $7x-10y+6=0.$
–Ґ–µ–њ–µ—А—М –љ–∞—Е–Њ–і–Є–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:
$(x-x_0)+f'(x_0)(y-y_0)=0\Rightarrow$ $(x-2)+\frac{7}{10}(y-2)=0\Rightarrow 10(x-2)+7(y-2)=0\Rightarrow 10x+7y-34=0.$
–Ю—В–≤–µ—В:¬†–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$7x-10y+6=0;$¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$10x+7y-34=0.$¬†
–Э–∞–є—В–Є —Г–≥–ї—Л, –њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ–Є –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –Ј–∞–і–∞–љ–љ—Л–µ –Ї—А–Є–≤—Л–µ:
5.254. $y=x^2$ –Є $y=x^3.$
–†–µ—И–µ–љ–Є–µ.
–£–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї—А–Є–≤—Л–Љ–Є –љ–∞—Е–Њ–і–Є–Љ –њ–Њ —Д–Њ—А–Љ—Г–ї–µ¬†$$tg\,\omega=\frac{f_2'(x_0)-f'_1(x_0)}{1+f'_1(x_0)f'_2(x_0)}.$$
–Э–∞–є–і–µ–Љ –Ї–Њ–Њ—А–і–Є–љ–∞—В—Л —В–Њ—З–Ї–Є –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П –Ј–∞–і–∞–љ–љ—Л—Е –Ї—А–Є–≤—Л—Е. –†–µ—И–∞–µ–Љ —Б–Є—Б—В–µ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є–є:
$\left\{\begin{array}{rcl} y=x^2,\\ y=x^3,\end{array}\right.\Rightarrow$¬†$\left\{\begin{array}{rcl} y=x^2,\\ x^2=x^3,\end{array}\right.\Rightarrow$¬†$\left\{\begin{array}{rcl} y=x^2,\\ x_1=0\\x_2=1,\end{array}\right.$ –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –Ї—А–Є–≤—Л–µ –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–∞—Е $M_1(0, 0)$ –Є $M_2(1, 1).$
–Ф–∞–ї–µ–µ –љ–∞–є–і–µ–Љ –Ј–љ–∞—З–µ–љ–Є—П –њ—А–Њ–Є–Ј–≤–Њ–і–љ—Л—Е –Ј–∞–і–∞–љ—Л—Е —Д—Г–љ–Ї—Ж–Є–є –≤ —В–Њ—З–Ї–∞—Е –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П.
$f_1(x)=x^2\Rightarrow f_1'(x)=2x$
$f_2(x)=x^3\Rightarrow f_2'(x)=3x^2$
$f_1'(0)=0;$
$f_2'(0)=0;$
 
$f_1'(1)=2;$
$f_2'(1)=3.$
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –љ–∞–є–і–µ–љ–љ—Л–µ –Ј–љ–∞—З–µ–љ–Є—П, –≤ —Д–Њ—А–Љ—Г–ї—Г –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —Г–≥–ї–∞:
 $$tg\,\omega_1=\frac{f_2'(0)-f'_1(0)}{1+f'_1(0)f'_2(0)}=\frac{0-0}{1+0}=0.$$  
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, $\omega_1=0.$
 $$tg\,\omega_2=\frac{f_2'(1)-f'_1(1)}{1+f'_1(1)f'_2(1)}=\frac{3-2}{1+2\cdot 3}=\frac{1}{7}.$$
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, $\omega_2=arctg\frac{1}{7}.$
–Ю—В–≤–µ—В: –Т —В–Њ—З–Ї–µ¬†$M_1(0, 0)$ —Г–≥–Њ–ї —А–∞–≤–µ–љ 0. (—В.–µ. –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ —Б–Њ–≤–њ–∞–і–∞—О—В), –≤¬†—В–Њ—З–Ї–µ¬†$M_2(1, 1)$ —Г–≥–Њ–ї —А–∞–≤–µ–љ $arctg\frac{1}{7}.$¬†
 
–Ф–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ.
–Э–∞–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Є –љ–Њ—А–Љ–∞–ї–Є –Ї –≥—А–∞—Д–Є–Ї—Г —Д—Г–љ–Ї—Ж–Є–Є $y=f(x)$ –≤ –і–∞–љ–љ–Њ–є —В–Њ—З–Ї–µ, –µ—Б–ї–Є:
5.236. $y=x^3+2x^2-4x-3,$ $x_0=-2.$
–Ю—В–≤–µ—В:¬†–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$y-5=0;$¬†¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$x+2=0.$
 
5.238. $y=tg 2x,\,\,\, x_0=0.$
–Ю—В–≤–µ—В:¬†–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$y-2x=0;$¬†¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$2y+x=0.$
 
5.239. $y=\ln x,\,\,\, x_0=1.$
–Ю—В–≤–µ—В:¬†–£—А–∞–≤–љ–µ–љ–Є–µ –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є:¬†$x-y-1=0;$¬†¬†—Г—А–∞–≤–љ–µ–љ–Є–µ –љ–Њ—А–Љ–∞–ї–Є:¬†$x+y-1=0.$
 
5.242. –Э–∞–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–∞—Б–∞—В–µ–ї—М–љ—Л—Е –Ї –Ї—А–Є–≤–Њ–є ¬†$$x=t\cos t, \,\,\, y=t\sin t,\,\,\, t\in(-\infty,\,\, +\infty),$$ –≤ –љ–∞—З–∞–ї–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В –Є –≤ —В–Њ—З–Ї–µ $t=\pi/4.$
–Ю—В–≤–µ—В:¬†$y=0,$¬†¬†¬†$(\pi+4)x+(\pi-4)y-\pi^2\frac{\sqrt 2}{4}=0$
 
5.244.¬†–Э–∞–њ–Є—Б–∞—В—М —Г—А–∞–≤–љ–µ–љ–Є—П –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є –Ї –Ї—А–Є–≤–Њ–є $$x^5+y^5-2xy=0 –≤ —В–Њ—З–Ї–µ $M_0(1, 1).$
–Ю—В–≤–µ—В:¬†$ x+y-2=0.$
 
–Э–∞–є—В–Є —Г–≥–ї—Л,–њ–Њ–і –Ї–Њ—В–Њ—А—Л–Љ–Є –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –Ј–∞–і–∞–љ–љ—Л–µ –Ї—А–Є–≤—Л–µ:
5.255. $y=(x-2)^2$ –Є $y=4x-x^2+4.$
–Ю—В–≤–µ—В:¬†$arctg\frac{8}{15}.$
 
5.256. $y=\sin x$ –Є $y=\cos x,\,\, x\in[0, 2\pi].$
–Ю—В–≤–µ—В:¬†$arctg2\sqrt 2.$
 
5.260. –Э–∞–є—В–Є —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –љ–∞—З–∞–ї–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В –і–Њ –љ–Њ—А–Љ–∞–ї–Є –Ї –ї–Є–љ–Є–Є $y=e^{2x}+x^2,$ –њ—А–Њ–≤–µ–і–µ–љ–љ–Њ–є –≤ —В–Њ—З–Ї–µ —Б –∞–±—Б—Ж–Є—Б—Б–Њ–є $x=0.$
–Ю—В–≤–µ—В:¬†$\frac{2}{\sqrt 5}.$
 


