–ü―Ä―è–Φ–Α―è –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β,¬†–≤―¹–Β–≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ―΄–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è.
English Version: Line in space, all possible equations.
 
–¦–Η―²–Β―Ä–Α―²―É―Ä–Α: –Γ–±–Ψ―Ä–Ϋ–Η–Κ –Ζ–Α–¥–Α―΅ –Ω–Ψ –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Β. –ß–Α―¹―²―¨ 1. –ü–Ψ–¥ ―Ä–Β–¥ –ê. –£. –ï―³–Η–Φ–Ψ–≤–Α, –ë. –ü. –î–Β–Φ–Η–¥–Ψ–≤–Η―΅–Α.
 
–Γ―É―â–Β―¹―²–≤―É―é―² ―²–Α–Κ–Η–Β ―³–Ψ―Ä–Φ―΄ –Ζ–Α–Ω–Η―¹–Η ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β:
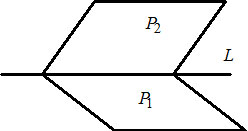
1)¬†$\left\{\begin{array}{lcl}A_1x+B_1y+C_1z+D_1=0\quad (P_1)\\ A_2x+B_2y+C_2z+D_2=0\quad (P_2)\end{array}\right. - $ –Ψ–±―â–Β–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι $L$ –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β, –Κ–Α–Κ –Μ–Η–Ϋ–Η–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –¥–≤―É―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι $P_1$ –Η $P_2.$
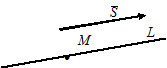
2) $\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} -$ ¬†–Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι $L,$ –Κ–Ψ―²–Ψ―Ä–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M(x_0, y_0, z_0)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $\overline{S}=(m, n, p).$ –£–Β–Κ―²–Ψ―Ä $\overline S$ ―è–≤–Μ―è–Β―²―¹―è –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Φ –≤–Β–Κ―²–Ψ―Ä–Ψ–Φ –Ω―Ä―è–Φ–Ψ–Ι $L.$
 
3)¬†$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1} -$¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Κ–Ψ―²–Ψ―Ä–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –¥–≤–Β ―²–Ψ―΅–Κ–Η $A(x_1, y_1, z_1)$ –Η $B(x_2, y_2, z_2).$¬†
4) –ü―Ä–Η―Ä–Α–≤–Ϋ–Η–≤–Α―è –Κ–Α–Ε–¥―É―é –Η–Ζ ―΅–Α―¹―²–Β–Ι –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–≥–Ψ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è 2 –Κ –Ω―Ä–Α―Ä–Α–Φ–Β―²―Ä―É $t,$ –Ω–Ψ–Μ―É―΅–Α–Β–Φ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι:
$$\left\{\begin{array}{lcl}x=x_0+mt\\ y=y_0+nt\\z=z_0+pt\end{array}\right.  $$
 
 
–†–Α―¹–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β –¥–≤―É―Ö –Ω―Ä―è–Φ―΄―Ö –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β.
 
–ü―É―¹―²―¨ $L_1:$¬†$\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1}$¬†$\overline{S}_1=(m_1, n_1, p_1);$
 
            $L_2:$ $\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2},$ $\overline{S}_2=(m_2, n_2, p_2).$
 
–Θ―¹–Μ–Ψ–≤–Η–Β –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ―¹―²–Η –¥–≤―É―Ö –Ω―Ä―è–Φ―΄―Ö:¬†–ü―Ä―è–Φ―΄–Β $L_1$ –Η $L_2$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ ―²–Ψ–≥–¥–Α –Η ―²–Ψ–Μ―¨–Κ–Ψ ―²–Ψ–≥–¥–Α, –Κ–Ψ–≥–¥–Α $\overline{S}_1\parallel\overline{S}_2\Leftrightarrow$¬†$\frac{m_1}{m_2}=\frac{n_1}{n_2}=\frac{p_1}{p_2}.$
 
–Θ―¹–Μ–Ψ–≤–Η–Β –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Ψ―¹―²–Η –¥–≤―É―Ö –Ω―Ä―è–Φ―΄―Ö:¬†$L_1\perp L_2\Leftrightarrow$¬†$\overline{S}_1\perp\overline{S}_2\Leftrightarrow$ ¬†${m_1}\cdot{m_2}+{n_1}\cdot{n_2}+p_1\cdot p_2=0.$
 
–Θ–≥–Ψ–Μ –Φ–Β–Ε–¥―É –Ω―Ä―è–Φ―΄–Φ–Η:
 $\cos\widehat{(L_1, L_2)}=$ $\frac{\overline{S}_1\cdot\overline{S}_2}{|\overline S_1|\cdot|\overline S_2|}=\frac{{m_1}\cdot{m_2}+{n_1}\cdot{n_2}+p_1\cdot p_2}{\sqrt{m_1^2+n_1^2+p_1^2}\cdot\sqrt{m_2^2+n_2^2+p_2^2}}.$
 
  
 
¬†–†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η –¥–Ψ –Ω―Ä―è–Φ–Ψ–Ι ―Ä–Α–≤–Ϋ–Ψ –¥–Μ–Η–Ϋ–Β –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Α, –Ψ–Ω―É―â–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Η–Ζ ―²–Ψ―΅–Κ–Η –Ϋ–Α –¥–Α–Ϋ–Ϋ―É―é –Ω―Ä―è–Φ―É―é.
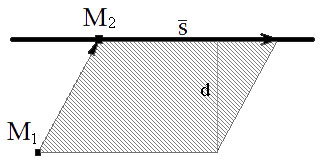
–ü―É―¹―²―¨ –Ω―Ä―è–Φ–Α―è $L$ –Ζ–Α–¥–Α–Ϋ–Α ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β–Φ $\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p},$ ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ $\overline S=(m, n, p).$ ¬†–ü―É―¹―²―¨ ―²–Α–Κ–Ε–Β $M_2=(x_2, y_2, z_2) -$ –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Α―è ―²–Ψ―΅–Κ–Α, –Ω―Ä–Η–Ϋ–Α–¥–Μ–Β–Ε–Α―â–Α―è –Ω―Ä―è–Φ–Ψ–Ι $L.$ –Δ–Ψ–≥–¥–Α ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η¬†$M_1=(x_1, y_1, z_1)$ –¥–Ψ –Ω―Ä―è–Φ–Ψ–Ι $L$ –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–Ι―²–Η –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β: $$d(M_1, L)=\frac{|[\overline{M_1M_2}, \overline S]|}{|\overline S|}.$$
–ü―Ä–Η–Φ–Β―Ä―΄.
2.198. –ù–Α–Ω–Η―¹–Α―²―¨ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M_0(2, 0, -3)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ:
–Α) –≤–Β–Κ―²–Ψ―Ä―É $q(2, -3, 5);$
–±) –Ω―Ä―è–Φ–Ψ–Ι $\frac{x-1}{5}=\frac{y+2}{2}=\frac{z+1}{-1};$
–≤) –Ψ―¹–Η $OX;$
–¥) –Ω―Ä―è–Φ–Ψ–Ι¬†$\left\{\begin{array}{lcl}3x-y+2z-7=0,\\ x+3y-2z-3=0; \end{array}\right. ¬†$
–Β) –Ω―Ä―è–Φ–Ψ–Ι $x=-2+t, y=2t, z=1-\frac{1}{2}t.$
–†–Β―à–Β–Ϋ–Η–Β.
–Α) –£–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è ―³–Ψ―Ä–Φ―É–Μ–Ψ–Ι (2) ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β:¬†
$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p} -$ ¬†–Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι $L,$ –Κ–Ψ―²–Ψ―Ä–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M(x_0, y_0, z_0)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $\overline{S}=(m, n, p).$
–ü–Ψ ―É―¹–Μ–Ψ–≤–Η―é¬†¬†$M_0(2, 0, -3)$ –Η¬†$\overline{S}=q(2,-3,5).$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ,¬†$\frac{x-2}{2}=\frac{y-0}{-3}=\frac{z-(-3)}{5}\Rightarrow\frac{x-2}{2}=\frac{y}{-3}=\frac{z+3}{5}.$
–û―²–≤–Β―²:¬†$\frac{x-2}{2}=\frac{y}{-3}=\frac{z+3}{5}.$
 
–±) –ü―Ä―è–Φ–Α―è, –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α―è –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι, –¥–Ψ–Μ–Ε–Ϋ–Α –±―΄―²―¨ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Α –Β–Β –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Β–Φ―É –≤–Β–Κ―²–Ψ―Ä―É. –ù–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ω―Ä―è–Φ–Ψ–Ι¬†¬†$\frac{x-1}{5}=\frac{y+2}{2}=\frac{z+1}{-1}$ –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $\overline S(5, 2, -1).$ –î–Α–Μ–Β–Β, –Ϋ–Α―Ö–Ψ–¥–Η–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι¬†―²–Ψ―΅–Κ―É $M_0(2, 0, -3)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É¬†$\overline S(5, 2, -1)$ –Κ–Α–Κ –Η –≤ –Ω―É–Ϋ–Κ―²–Β –Α):
$\frac{x-2}{5}=\frac{y-0}{2}=\frac{z-(-3)}{-1}\Rightarrow\frac{x-2}{5}=\frac{y}{2}=\frac{z+3}{-1}.$
–û―²–≤–Β―²:¬†$\frac{x-2}{5}=\frac{y}{2}=\frac{z+3}{-1}.$
 
–≤) –Ψ―¹―¨ OX –Η–Φ–Β–Β―² –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä $i=(1, 0, 0).$ –Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Η―â–Β–Φ¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι¬†―²–Ψ―΅–Κ―É $M_0(2, 0, -3)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $i(1, 0, 0):$
$\frac{x-2}{1}=\frac{y-0}{0}=\frac{z-(-3)}{0}\Rightarrow\frac{x-2}{1}=\frac{y}{0}=\frac{z+3}{0}.$
–û―²–≤–Β―²:¬†$\frac{x-2}{1}=\frac{y}{0}=\frac{z+3}{0}.$
 
–¥) –ü―Ä―è–Φ–Α―è, –Ζ–Α–¥–Α–Ϋ–Ϋ–Α―è –Κ–Α–Κ –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η–Β –¥–≤―É―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α –Ϋ–Ψ―Ä–Φ–Α–Μ―è–Φ –Ψ–±–Β–Η―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι, –Ω–Ψ―ç―²–Ψ–Φ―É¬†–ù–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä¬†–Ω―Ä―è–Φ–Ψ–Ι¬†
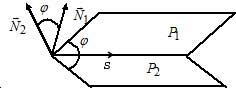
$\left\{\begin{array}{lcl}3x-y+2z-7=0,\\ x+3y-2z-3=0; \end{array}\right.$ –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–Ι―²–Η –Κ–Α–Κ –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ϋ–Ψ―Ä–Φ–Α–Μ–Β–Ι –Ζ–Α–¥–Α–Ϋ–Ϋ―΄―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι.
–î–Μ―è –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P_1:$ $3x-y+2z-7=0$ –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―΄–Ι –≤–Β–Κ―²–Ψ―Ä –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $N_1(3, -1, 2);$
–¥–Μ―è –Ω–Μ–Ψ―¹–Ψ―¹―²–Η $P_2:$ $x+3y-2z-3,$ –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―΄–Ι –≤–Β–Κ―²–Ψ―Ä –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $N_2(1, 3, -2).$
–ù–Α―Ö–Ψ–¥–Η–Φ –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β:
$[N_1, N_2]=\begin{vmatrix}i&j&k\\3&-1&2\\1&3&-2\end{vmatrix}=i(2-6)-j(-6-2)+k(9+1)=-4i+8j+10k.$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ω―Ä―è–Φ–Ψ–Ι¬†$\left\{\begin{array}{lcl}3x-y+2z-7=0,\\ x+3y-2z-3=0; \end{array}\right.$ –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $\overline S (-4, 8, 10).$
–î–Α–Μ–Β–Β –Ϋ–Α–Φ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Ϋ–Α–Ι―²–Η¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι¬†―²–Ψ―΅–Κ―É $M_0(2, 0, -3)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $\overline S(-4, 8, 10):$
 $\frac{x-2}{-4}=\frac{y-0}{8}=\frac{z-(-3)}{10}\Rightarrow\frac{x-2}{-4}=\frac{y}{8}=\frac{z+3}{10}.$
¬†–û―²–≤–Β―²:¬†$\frac{x-2}{-4}=\frac{y}{8}=\frac{z+3}{10}.$
  {jumi[*4]}
–Β) –ù–Α–Ι–¥–Β–Φ –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ω―Ä―è–Φ–Ψ–Ι¬†¬†$x=-2+t, y=2t, z=1-\frac{1}{2}t.$ –î–Μ―è ―ç―²–Ψ–≥–Ψ –Ζ–Α–Ω–Η―à–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―ç―²–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι –≤ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Φ –≤–Η–¥–Β:
$\left\{\begin{array}{lcl}x=-2+t,\\ y=2t,\\z=1-\frac{1}{2}t \end{array}\right.\Rightarrow$ $\left\{\begin{array}{lcl}t=x+2,\\ t=\frac{y}{2},\\t=\frac{z-1}{-\frac{1}{2}} \end{array}\right.$ $\Rightarrow\frac{x+2}{1}=\frac{y}{2}=\frac{z-1}{-\frac{1}{2}}.$
–û―²―¹―é–¥–Α –Ϋ–Α―Ö–Ψ–¥–Η–Φ –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä $\overline S\left(1, 2, -\frac{1}{2}\right).$ –Θ–Φ–Ϋ–Ψ–Ε–Η–Φ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Β–≥–Ψ –≤–Β–Κ―²–Ψ―Ä–Α –Ϋ–Α 2 (―΅―²–Ψ–±―΄ –Η–Ζ–±–Α–≤–Η―²―¨―¹―è –Ψ―² –¥―Ä–Ψ–±–Η): $\overline S_1(2, 4, -1).$
–î–Α–Μ–Β–Β –Ϋ–Α–Φ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Ϋ–Α–Ι―²–Η¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι¬†―²–Ψ―΅–Κ―É $M_0(2, 0, -3)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $\overline S(2, 4, -1):$
$\frac{x-2}{2}=\frac{y-0}{4}=\frac{z-(-3)}{-1}\Rightarrow\frac{x-2}{2}=\frac{y}{4}=\frac{z+3}{-1}.$
–û―²–≤–Β―²:¬†$\frac{x-2}{2}=\frac{y}{4}=\frac{z+3}{-1}.$
 
2.199(a). –ù–Α–Ω–Η―¹–Α―²―¨ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ –¥–≤–Β –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Β ―²–Ψ―΅–Κ–Η $M_1 (1, -2, 1)$ –Η $M_2(3, 1, -1).$¬†
–†–Β―à–Β–Ϋ–Η–Β.
–£–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è ―³–Ψ―Ä–Φ―É–Μ–Ψ–Ι (3)¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β:
$\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1} -$¬†―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Κ–Ψ―²–Ψ―Ä–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ –¥–≤–Β ―²–Ψ―΅–Κ–Η $A(x_1, y_1, z_1)$ –Η $B(x_2, y_2, z_2).$¬†
–ü–Ψ–¥―¹―²–Α–≤–Μ―è–Β–Φ –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Β ―²–Ψ―΅–Κ–Η:¬†
$\frac{x-1}{3-1}=\frac{y+2}{1+2}=\frac{z-1}{-1-1} \Rightarrow$ $\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-1}{-2}.$
–û―²–≤–Β―²:¬†$\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-1}{-2}.$
 
2.204. –ù–Α–Ι―²–Η ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Φ–Β–Ε–¥―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄–Φ–Η –Ω―Ä―è–Φ―΄–Φ–Η
$\frac{x-2}{3}=\frac{y+1}{4}=\frac{z}{2}$ –Η¬†$\frac{x-7}{3}=\frac{y-1}{4}=\frac{z-3}{2}.$
–†–Β―à–Β–Ϋ–Η–Β.
–†–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Φ–Β–Ε–¥―É –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄–Φ–Η –Ω―Ä―è–Φ―΄–Φ–Η $L_1$ –Η $L_2$ ¬†―Ä–Α–≤–Ϋ–Ψ ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η―é –Ψ―² –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Ψ–Ι ―²–Ψ―΅–Κ–Η –Ω―Ä―è–Φ–Ψ–Ι $L_1$ –¥–Ψ –Ω―Ä―è–Φ–Ψ–Ι $L_2.$ –Γ–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ, –Β–≥–Ψ –Φ–Ψ–Ε–Ϋ–Ψ –Ϋ–Α–Ι―²–Η –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Β¬†$$d(L_1, L_2)=d(M_1, L_2)=\frac{|[\overline{M_1M_2}, \overline S]|}{|\overline S|},$$ –≥–¥–Β $M_1-$ –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Α―è ―²–Ψ―΅–Κ–Α –Ω―Ä―è–Φ–Ψ–Ι $L_1,$ $M_2 - $–Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ–Α―è ―²–Ψ―΅–Κ–Α –Ω―Ä―è–Φ–Ψ–Ι $L_2,$ $\overline S -$ –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ω―Ä―è–Φ–Ψ–Ι $L_2.$
–‰–Ζ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Η―Ö ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Ι –Ω―Ä―è–Φ―΄―Ö –±–Β―Ä–Β–Φ ―²–Ψ―΅–Κ–Η $M_1=(2, -1, 0)\in L_1,$ $M_2=(7, 1, 3)\in L_2,$ $\overline S=(3, 4, 2).$
–û―²―¹―é–¥–Α –Ϋ–Α―Ö–Ψ–¥–Η–Φ $\overline{M_1M_2}=(7-2, 1-(-1),3-0)=(5, 2, 3);$
$[\overline{M_1M_2}, \overline S]=\begin{vmatrix}i&j&k\\5&2&3\\3&4&2\end{vmatrix}=i(4-12)-j(10-9)+k(20-6)=$ $=-8i-j+14k.$
$|[\overline{M_1M_2},\overline S]|=\sqrt{8^2+1+14^2}=\sqrt{64+1+196}=\sqrt{261}=\sqrt{9* 29}=3\sqrt{29}.$
$|\overline S|=\sqrt{3^2+4^2+2^2}=\sqrt{9+16+4}=\sqrt{29}$
$$d(L_1, L_2)=\frac{|[\overline{M_1M_2}, \overline S]|}{|\overline S|}=\frac{3\sqrt{29}}{\sqrt{29}}=3.$$
–û―²–≤–Β―²: 3.
 
¬†2.205 (–Α). –ù–Α–Ι―²–Η ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η $A(2, 3, -1)$ –¥–Ψ –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι¬†$L:$¬†$\left\{\begin{array}{lcl}2x-2y+z+3=0,\\ 3x-2y+2z+17=0 \end{array}\right.$
–†–Β―à–Β–Ϋ–Η–Β.
–î–Μ―è ―²–Ψ–≥–Ψ, ―΅―²–Ψ–±―΄ –Ϋ–Α–Ι―²–Η ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η $A$¬†–¥–Ψ –Ω―Ä―è–Φ–Ψ–Ι $L,$¬†–Ϋ–Α–Φ –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –≤―΄–±―Ä–Α―²―¨ –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ―¨–Ϋ―É―é ―²–Ψ―΅–Κ―É $M,$ –Ω―Ä–Η–Ϋ–Α–¥–Μ–Β–Ε–Α―â―É―é –Ω―Ä―è–Φ–Ψ–Ι $L$ –Η –Ϋ–Α–Ι―²–Η –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä ―ç―²–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι.
–£―΄–±–Η―Ä–Α–Β–Φ ―²–Ψ―΅–Κ―É $M.$ –ü―É―¹―²―¨ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Α $z=0.$ –ü–Ψ–¥―¹―²–Α–≤–Η–Φ ―ç―²–Ψ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –≤ –¥–Α–Ϋ–Ϋ―É―é ―¹–Η―¹―²–Β–Φ―É:¬†
$\left\{\begin{array}{lcl}2x-2y+0+3=0,\\ 3x-2y+0+17=0 \end{array}\right.\Rightarrow$ $\left\{\begin{array}{lcl}2x-2y+3=0,\\ 3x-2y+17=0 \end{array}\right.-\Rightarrow$ $\left\{\begin{array}{lcl}x+14=0,\\ 2x-2y+3=0 \end{array}\right.\Rightarrow$ $\left\{\begin{array}{lcl}x=-14,\\ -28-2y+3=0 \end{array}\right.\Rightarrow$ $\left\{\begin{array}{lcl}x=-14,\\ y=-\frac{25}{2}. \end{array}\right.$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, $M=(-14, -\frac{25}{2}, 0)$
–ù–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ϋ–Α–Ι–¥–Β–Φ, –Κ–Α–Κ –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ϋ–Ψ―Ä–Φ–Α–Μ–Β–Ι –Ζ–Α–¥–Α–Ϋ–Ϋ―΄―Ö –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Β–Ι:
–î–Μ―è –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P_1:$ $2x-2y+z+3=0$ –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―΄–Ι –≤–Β–Κ―²–Ψ―Ä –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $N_1(2, -2, 1);$
–¥–Μ―è –Ω–Μ–Ψ―¹–Ψ―¹―²–Η $P_2:$ $3x+2y+2z+17=0,$ –Ϋ–Ψ―Ä–Φ–Α–Μ―¨–Ϋ―΄–Ι –≤–Β–Κ―²–Ψ―Ä –Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $N_2(3, -2, 2).$
–ù–Α―Ö–Ψ–¥–Η–Φ –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ–Β –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β:
$[N_1, N_2]=\begin{vmatrix}i&j&k\\2&-2&1\\3&-2&2\end{vmatrix}=i(-4+2)-j(4-3)+k(-4+6)=-2i-j+2k.$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ϋ–Α–Ω―Ä–Α–≤–Μ―è―é―â–Η–Ι –≤–Β–Κ―²–Ψ―Ä –Ω―Ä―è–Φ–Ψ–Ι¬†$\left\{\begin{array}{lcl}2x-2y+z+3=0,\\ 3x-2y+2z+17=0 \end{array}\right.$
–Η–Φ–Β–Β―² –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ $\overline S (-2, -1, 2).$
–Δ–Β–Ω–Β―Ä―¨ –Φ–Ψ–Ε–Ϋ–Ψ –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è ―³–Ψ―Ä–Φ―É–Μ–Ψ–Ι $$d(A, L)=\frac{|[\overline{AM}, \overline S]|}{|\overline S|}.$$
$\overline{AM}=\left(2-(-14),3-\left(-\frac{25}{2}\right),-1-0\right)=\left(16, 15\frac{1}{2}, -1\right)$
$[\overline{AM}, \overline S]=\begin{vmatrix}i&j&k\\16&15,5&-1\\-2&-1&2\end{vmatrix}=i(31-1)-j(32-2)+k(-16+31)=$ $=30i-30j+15k.$
 $|[\overline{AM},\overline S]|=\sqrt{30^2+30^2+15^2}=\sqrt{900+900+225}=\sqrt{2025}=45.$
 $|\overline S|=\sqrt{2^2+1^2+2^2}=\sqrt{4+1+4}=3$
 $$d(A, L)=\frac{|[\overline{AM}, \overline S]|}{|\overline S|}=\frac{45}{3}=15.$$
¬†–û―²–≤–Β―²:¬†$d(A, L)=15.$
 
2.212. –ù–Α–Ω–Η―¹–Α―²―¨ –Κ–Α–Ϋ–Ψ–Ϋ–Η―΅–Β―¹–Κ–Ψ–Β ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Κ–Ψ―²–Ψ―Ä–Α―è –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M_0(3, -2, -4)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P: 3x-2y-3z-7=0$ –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α–Β―² –Ω―Ä―è–Φ―É―é $L: \frac{x-2}{3}=\frac{y+4}{-2}=\frac{z-1}{2}.$
–†–Β―à–Β–Ϋ–Η–Β.¬†
–½–Α–Ω–Η―à–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P_1,$ –Κ–Ψ―²–Ψ―Ä–Α―謆–Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M_0(3, -2, -4)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $3x-2y-3z-7=0:$
$P: 3x-2y-3z-7=0\Rightarrow \overline N=(3; -2; -3).$ –‰―¹–Κ–Ψ–Φ–Α―è –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²―¨ –Ω―Ä–Ψ―Ö–Ψ–¥–Η―² ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M_0(3, -2, -4)$ –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Ψ –≤–Β–Κ―²–Ψ―Ä―É $\overline N(3, -2, -3).$
$P_1: 3(x-3)-2(y+2)-3(z+4)=0\Rightarrow $
$P_1: 3x-9-2y-4-3z-12=0 \Rightarrow$
$P_1: 3x-2y-3z-25=0.$
–î–Α–Μ–Β–Β –Ϋ–Α–Ι–¥–Β–Φ ―²–Ψ―΅–Κ―É –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P_1$ –Η –Ω―Ä―è–Φ–Ψ–Ι $L.$ –î–Μ―è ―ç―²–Ψ–≥–Ψ –Ζ–Α–Ω–Η―à–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι $L$ –≤ –Ω–Α―Ä–Α–Φ–Β―²―Ä–Η―΅–Β―¹–Κ–Ψ–Ι ―³–Ψ―Ä–Φ–Β:¬†
$L: \frac{x-2}{3}=\frac{y+4}{-2}=\frac{z-1}{2}=t\Rightarrow$
 $\left\{\begin{array}{lcl}x=3t+2,\\ y=-2t-4,\\z=2t+1. \end{array}\right.$
–î–Α–Μ–Β–Β, –Ω–Ψ–¥―¹―²–Α–≤–Η–Φ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è $x, y$ ¬†–Η $z,$ –≤―΄―Ä–Α–Ε–Β–Ϋ–Ϋ―΄–Β ―΅–Β―Ä–Β–Ζ $t$ –≤ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $P_1,$ –Η –Η–Ζ –Ω–Ψ–Μ―É―΅–Β–Ϋ–Ϋ–Ψ–≥–Ψ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –≤―΄―Ä–Α–Ζ–Φ $t:$
$3x-2y-3z-25=0$
$3(3t+2)-2(-2t-4)-3(2t+1)-25=0$
$9t+6+4t+8-6t-3-25=0$
$7t-14=0$
$t=\frac{14}{7}=2$
–ü–Ψ–¥―¹―²–Α–≤–Μ―è―è –Ϋ–Α–Ι–¥–Β–Ϋ–Ϋ–Ψ–Β –Ζ–Α–Ϋ―΅–Β–Ϋ–Η–Β $t$ –≤ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι $L,$ –Ϋ–Α–Ι–¥–Β–Φ –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²―΄ ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è:
  $\left\{\begin{array}{lcl}x=3t+2,\\ y=-2t-4,\\z=2t+1. \end{array}\right.\Rightarrow $  $\left\{\begin{array}{lcl}x=6+2=8,\\ y=-4-4=-8,\\z=4+1=5. \end{array}\right.$
–Δ–Α–Κ–Η–Φ –Ψ–±―Ä–Α–Ζ–Ψ–Φ, –Ω―Ä―è–Φ–Α―è $L$ –Η –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²―¨ $P_1$ –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β $M_1(8, -8, 5).$
–Δ–Β–Ω–Β―Ä―¨ –Ζ–Α–Ω–Η―à–Β–Φ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η $M_0(3, -2. -4)$ –Η $M_1(8, -8, 5)$-- ―ç―²–Ψ –Η –±―É–¥–Β―² –Η―¹–Κ–Ψ–Φ–Α―è –Ω―Ä―è–Φ–Α―è.¬†–£–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è ―³–Ψ―Ä–Φ―É–Μ–Ψ–Ι (3) $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1} :$
$\frac{x-3}{8-3}=\frac{y+2}{-8+2}=\frac{z+4}{5+4}\Rightarrow$ $\frac{x-3}{5}=\frac{y+2}{-6}=\frac{z+4}{9}.$
¬†–û―²–≤–Β―²:¬†$\frac{x-3}{5}=\frac{y+2}{-6}=\frac{z+4}{9}.$
 
 
–î–Ψ–Φ–Α―à–Ϋ–Β–Β –Ζ–Α–¥–Α–Ϋ–Η–Β.
2.199.
–±)¬†¬†–ù–Α–Ω–Η―¹–Α―²―¨ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ –¥–≤–Β –Ζ–Α–¥–Α–Ϋ–Ϋ―΄–Β ―²–Ψ―΅–Κ–Η $M_1 (3, -1, 0)$ –Η $M_2(1, 0, -3).$¬†
–û―²–≤–Β―²:¬†$\frac{x-3}{-2}=\frac{y+1}{1}=\frac{z}{-3}.$
 
2.205.
–±)¬†–ù–Α–Ι―²–Η ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β –Ψ―² ―²–Ψ―΅–Κ–Η $A(2, 3, -1)$ –¥–Ψ –Ζ–Α–¥–Α–Ϋ–Ϋ–Ψ–Ι –Ω―Ä―è–Φ–Ψ–Ι¬†$L:$¬†$\left\{\begin{array}{lcl}x=3t+5,\\ y=2t,\\z=-2t-25. \end{array}\right.$
–û―²–≤–Β―²: 21.
 
2.206. –î–Ψ–Κ–Α–Ζ–Α―²―¨, ―΅―²–Ψ –Ω―Ä―è–Φ―΄–Β¬†$L_1: \left\{\begin{array}{lcl}2x+2y-z-10=0,\\ x-y-z-22=0, \end{array}\right.$ –Η¬†$L_2: \frac{x+7}{3}=\frac{y-5}{-1}=\frac{z-9}{4}.$¬†–Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ―΄ –Η –Ϋ–Α–Ι―²–Η ―Ä–Α―¹―¹―²–Ψ―è–Ϋ–Η–Β $\rho(L_1, L_2)$
–û―²–≤–Β―²: 25.
 
2.207. –Γ–Ψ―¹―²–Α–≤–Η―²―¨ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η―è –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ–Η –Ω–Β―Ä–Β―¹–Β―΅–Β–Ϋ–Η―è –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $x-3y+2z+1=0$ ―¹ –Ω―Ä―è–Φ―΄–Φ–Η $\frac{x-5}{5}=\frac{y+1}{-2}=\frac{z-3}{-1}$ –Η $\frac{x-3}{4}=\frac{y+4}{-6}=\frac{z-5}{2}.$
–û―²–≤–Β―²:¬†$\frac{x+1}{7}=\frac{y-2}{-1}=\frac{z-3}{-5}.$
 
2.211. –ù–Α–Ω–Η―¹–Α―²―¨ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ω―Ä―è–Φ–Ψ–Ι, –Ω―Ä–Ψ―Ö–Ψ–¥―è―â–Β–Ι ―΅–Β―Ä–Β–Ζ ―²–Ψ―΅–Κ―É $M_0(7, 1, 0)$ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ―¨–Ϋ–Ψ –Ω–Μ–Ψ―¹–Κ–Ψ―¹―²–Η $2x+3y-z-15=0$ –Η –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―â–Β–Ι –Ω―Ä―è–Φ―É―é $\frac{x}{1}=\frac{y-1}{4}=\frac{z-3}{2}.$
¬†–û―²–≤–Β―²:¬†$\frac{x-7}{67}=\frac{y-1}{-28}=\frac{z}{70}.$
 
{jcomments on}
 

