–Я—А—П–Љ–∞—П –љ–∞ –њ–ї–Њ—Б–Ї–Њ—Б—В–Є, –≤—Б–µ–≤–Њ–Ј–Љ–Њ–ґ–љ—Л–µ —Г—А–∞–≤–љ–µ–љ–Є—П.
–Ы–Є—В–µ—А–∞—В—Г—А–∞: –°–±–Њ—А–љ–Є–Ї –Ј–∞–і–∞—З –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ. –І–∞—Б—В—М 1. –Я–Њ–і —А–µ–і –Р. –Т. –Х—Д–Є–Љ–Њ–≤–∞, –С. –Я. –Ф–µ–Љ–Є–і–Њ–≤–Є—З–∞.
 
–°—Г—Й–µ—Б—В–≤—Г—О—В —В–∞–Ї–Є–µ —Д–Њ—А–Љ—Л –Ј–∞–њ–Є—Б–Є —Г—А–∞–≤–љ–µ–љ–Є—П –њ—А—П–Љ–Њ–є:
1) $y=kx+b,$ –≥–і–µ $k -$ —Г–≥–ї–Њ–≤–Њ–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В, $b-$ –Њ—В—А–µ–Ј–Њ–Ї, –Ї–Њ—В–Њ—А—Л–є –њ—А—П–Љ–∞—П –Њ—В—Б–µ–Ї–∞–µ—В –љ–∞ –Њ—Б–Є $OY.$
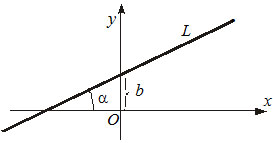
2) $y-y_0=k(x-x_0) $ - —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є, –Ї–Њ—В–Њ—А–∞—П –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –Ј–∞–і–∞–љ–љ—Г—О —В–Њ—З–Ї—Г $P(x_0, y_0)$ –њ–Њ–і –Ј–∞–і–∞–љ–љ—Л–Љ —Г–≥–ї–Њ–Љ $\alpha$ –Ї –Њ—Б–Є $OX$ $(k=tg\alpha).$
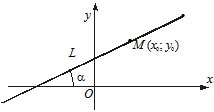
3) $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} $ - —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є, –Ї–Њ—В–Њ—А–∞—П –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј –і–≤–µ —В–Њ—З–Ї–Є $M(x_1, y_1)$ –Є $N(x_2, y_2).$¬†
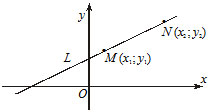
4) $\frac{x}{a}+\frac{y}{b}=1 $ - —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є –≤ –Њ—В—А–µ–Ј–Ї–∞—Е –љ–∞ –Њ—Б—П—Е, –≥–і–µ $a$ –Є $b -$ –≤–µ–ї–Є—З–Є–љ—Л –Њ—В—А–µ–Ј–Ї–Њ–≤, –Ї–Њ—В–Њ—А—Л–µ –њ—А—П–Љ–∞—П –Њ—В—Б–µ–Ї–∞–µ—В –љ–∞ –Њ—Б—П—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В.
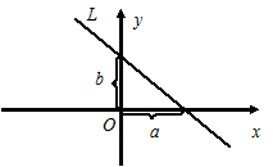
5) $\frac{x-x_0}{l}=\frac{y-y_0}{m} $ - –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є, –≥–і–µ $\overline{S}=(l, m) -$ –љ–∞–њ—А–∞–≤–ї—П—О—Й–Є–є –≤–µ–Ї—В–Њ—А –њ—А—П–Љ–Њ–є, —В–Њ –µ—Б—В—М –≤–µ–Ї—В–Њ—А –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–є –њ—А—П–Љ–Њ–є $(\overline{S}\parallel L),$ —В–Њ—З–Ї–∞ $P(x_0, y_0)\in L.$
  {jumi[*4]}
6) $A(x-x_0)+B(y-y_0)=0$ - —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є $L,$ –Ї–Њ—В–Њ—А–∞—П –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —В–Њ—З–Ї—Г $M(x_0, y_0)$ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Њ –≤–µ–Ї—В–Њ—А—Г $\overline{N}=(A, B).$ –Т–µ–Ї—В–Њ—А $\overline N$ –љ–∞–Ј—Л–≤–∞–µ—В—Б—П –љ–Њ—А–Љ–∞–ї—М–љ—Л–Љ –≤–µ–Ї—В–Њ—А–Њ–Љ –њ—А—П–Љ–Њ–є.
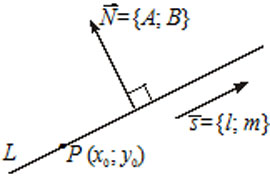
7) $Ax+By+C=0 -$ –Њ–±—Й–µ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є $L,$ –≥–і–µ $\overline{N}=(A, B) -$ –љ–Њ—А–Љ–∞–ї—М–љ—Л–є –≤–µ–Ї—В–Њ—А –њ—А—П–Љ–Њ–є $L.$
8) $x\cos\alpha+y\cos\beta-p=0 -$ –љ–Њ—А–Љ–∞–ї—М–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є, –≥–і–µ $\cos\alpha$ –Є $\cos\beta -$ –љ–∞–њ—А–∞–≤–ї—П—О—Й–Є–µ –Ї–Њ—Б–Є–љ—Г—Б—Л –љ–Њ—А–Љ–∞–ї—М–љ–Њ–≥–Њ –≤–µ–Ї—В–Њ—А–∞ $n,$ –љ–∞–њ—А–∞–≤–ї–µ–љ–љ–Њ–≥–Њ –Є–Ј –љ–∞—З–∞–ї–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В –≤ —Б—В–Њ—А–Њ–љ—Г –њ—А—П–Љ–Њ–є, –∞ $p>0 -$ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В –љ–∞—З–∞–ї–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В –і–Њ –њ—А—П–Љ–Њ–є.
–Ю–±—Й–µ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ –њ—А—П–Љ–Њ–є –њ—А–Є–≤–Њ–і–Є—В—Б—П –Ї –љ–Њ—А–Љ–∞–ї—М–љ–Њ–Љ—Г, –њ—Г—В–µ–Љ —Г–Љ–љ–Њ–ґ–µ–љ–Є—П –љ–∞ –љ–Њ—А–Љ–Є—А—Г—О—Й–Є–є –Љ–љ–Њ–ґ–Є—В–µ–ї—М $\mu=-\frac{sgn C}{\sqrt{A^2+B^2}}.$
 
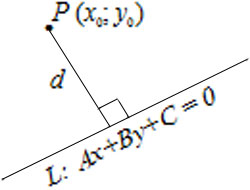
–†–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є $P(x_0, y_0)$ –і–Њ –њ—А—П–Љ–Њ–є $L: Ax+By+C=0$ –≤—Л—З–Є—Б–ї—П–µ—В—Б—П –њ–Њ —Д–Њ—А–Љ—Г–ї–µ $$d=\left|\frac{Ax_0+By_0+C}{\sqrt{A^2+B^2}}\right|.$$
 
- –Э–∞–Ј–∞–і
- –Т–њ–µ—А—С–і >>


